Кривая, являющаяся графиком функцииy=sinx, называется синусоидой.

Свойства функции y = sin(x) и её график

Теория:

Функция y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 2π.

График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например, на отрезке [0;π].

Однако проще применить формулу sinx=cos(x−π2), которая показывает, что график функции y=sinx можно получить сдвигом графика функции y=cosx вдоль оси абсцисс вправо на π2.

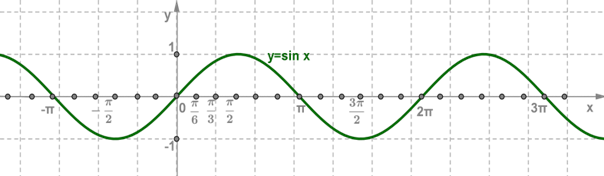
График функции y=sinx

Кривая, являющаяся графиком функцииy=sinx, называется синусоидой.

Свойства функции y=sinx

1. Область определения — множество R всех действительных чисел.

2. Множество значений — отрезок [−1;1].

3. Функция y=sinx периодическая с периодом T= 2π.

4. Функция y=sinx — нечётная.

5. Функция y=sinx принимает:
- значение, равное 0, при x=πn,n∈Z;
- наибольшее значение, равное 1, при x=π2+2πn,n∈Z;
- наименьшее значение, равное −1, при x=−π2+2πn,n∈Z;
- положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z;

- отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z.

6. Функция y=sinx:

- возрастает на отрезке

[−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z;
- убывает на отрезке

[π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z.

Свойства функции y = cosx и её график

Теория:

Функция y=cosx определена на всей числовой прямой, и множеством её значений является отрезок [−1;1].

Следовательно, график этой функции расположен в полосе между прямыми y=−1 и y=1.

Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например, на отрезке −π≤x≤π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn,n∈Z, график будет таким же.

Функция y=cosx является чётной. Поэтому её график симметричен относительно оси Oy.

Для построения графика на отрезке −π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси Oy.

Найдём несколько точек, принадлежащих графику на этом отрезке 0≤x≤π: cos0=1;cosπ6=3–√2;cosπ4=2–√2;cosπ3=12;cosπ2=0;cosπ=−1.

Итак, график функции y=cosx построен на всей числовой прямой.

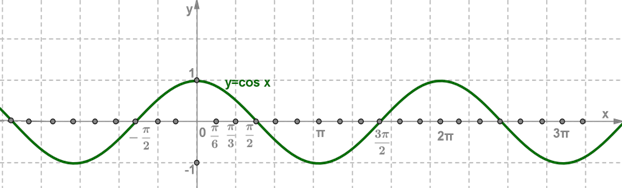
Свойства функции y=cosx

1. Область определения — множество R всех действительных чисел.

2. Множество значений — отрезок [−1;1].

3. Функция y=cosx периодическая с периодом 2π.

4. Функция y=cosx — чётная.

5. Функция y=cosx принимает:

- значение, равное 0, при x=π2+πn,n∈Z;

- наибольшее значение, равное 1, при x=2πn,n∈Z;

- наименьшее значение, равное −1, при x=π+2πn,n∈Z;

- положительные значения на интервале (−π2;π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z;

- отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z.

6. Функция y=cosx:

- возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z;

- убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z.

Функция y = tg(x) и её свойства

Теория:

Функция y=tgx определена при x≠π2+πn,n∈Z, является нечётной и периодической с периодом π.

Поэтому достаточно построить её график на промежутке [0;π2).

Выберем для построения контрольные точки, через которые проведём плавную кривую на координатной плоскости:

tg0=0;tgπ6=3−−√3;tgπ4=1;tgπ3=3–√.

Затем, отобразив её симметрично относительно начала координат, получим график на интервале (−π2;π2).

Используя периодичность, строим график функции y=tgx на всей области определения.

График функции y=tgx называют тангенсоидой.

Главной ветвью графика функции y=tgx обычно называют ветвь, заключённую в полосе (−π2;π2).

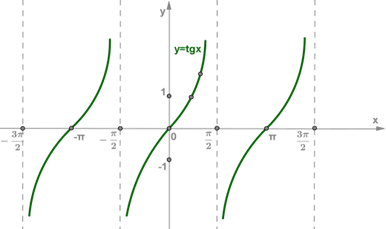
Свойства функции y=tgx

1. Область определения — множество всех действительных чисел x≠π2+πn,n∈Z.

2. Множество значений — множество R всех действительных чисел.

3. Функция y=tgx периодическая с периодом π.

4. Функция y=tgx нечётная.

5. Функция y=tgx принимает:

- значение 0 при x=πn,n∈Z;

- положительные значения на интервалах (πn;π2+πn),n∈Z;

- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.

6. Функция y=tgx возрастает на интервалах (−π2+πn;π2+πn),n∈Z.

Функция y = ctg(x) и её свойства

Теория:

Функция y=ctgx определена при x≠πn,n∈Z, является нечётной и периодической с периодом π.

Рассуждая аналогично, как при построении графика функции y=tgx, можно построить график функции y=ctgx.

График функции y=ctgx, как и график функции y=tgx, называют тангенсоидой.

Главной ветвью графика функции y=ctgx обычно называют ветвь, заключённую в полосе от x=0 до x= π.

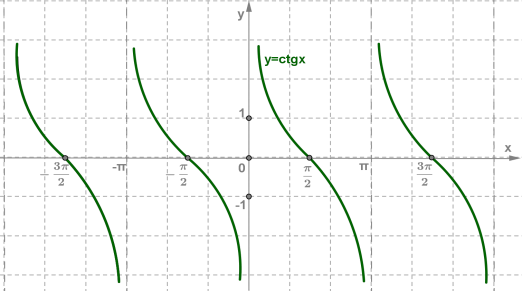
Свойства функции y=ctgx

1. Область определения — множество всех действительных чисел x≠πn,n∈Z.

2. Множество значений — множество R всех действительных чисел.

3. Функция y=ctgx периодическая с периодом π.

4. Функция y=ctgx нечётная.

5. Функция y=ctgx принимает:

- значение 0 при x=π2+πn,n∈Z;

- положительные значения на интервалах (πn;π2+πn),n∈Z;

- отрицательные значения на интервалах (−π2+πn;πn),n∈Z.

6. Функция y=ctgx убывает на интервалах (πn;π+πn),n∈Z.