
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Погрешности арифметических действий.
Теория погрешностей и машинная арифметика
Пусть 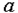 - точное значение,
- точное значение,
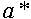 - приближенное значение некоторой величины.
- приближенное значение некоторой величины.
Абсолютной погрешностью приближенного значения 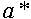 называется величина
называется величина 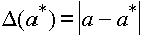 .
.
Относительной погрешностью значения 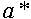 (при
(при 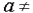 0) называется величина
0) называется величина 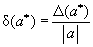 .
.
Так как, значение 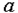 как правило неизвестно, чаще получают оценки погрешностей вида:
как правило неизвестно, чаще получают оценки погрешностей вида: 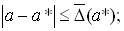
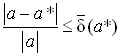 .
.
Величины 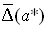 и
и 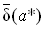 называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
Пример 1. Абсолютная и относительная погрешности приближенного числа e.
Число e - трансцендентное число, представляется бесконечной непериодической дробью e = 2.71828. Приближенное значение числа e* = 2.7. Граница абсолютной погрешности | e - e* | < 0.019, относительная погрешность числа
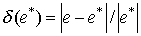 ,
, 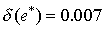
------------------------------------------------------------------------------------------------------------
Значащими цифрами числа 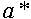 называют все цифры в его записи, начиная с первой ненулевой слева.
называют все цифры в его записи, начиная с первой ненулевой слева.
Пример 2. Значащие цифры числа.
Значащие цифры чисел подчеркнуты: 0.03589, 10.4920, 0.00456200.
------------------------------------------------------------------------------------------------------------
Значащую цифру числа 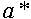 называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Пример 3. Верные цифры числа.
Верные цифры числа a = 356.78245 подчеркнуты.
Если 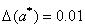 , то верных цифр в числе 5: a = 356.78245.
, то верных цифр в числе 5: a = 356.78245.
Если 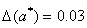 , то верных цифр в числе 4: a = 356.78245.
, то верных цифр в числе 4: a = 356.78245.
Если 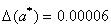 , то верных цифр в числе 7: a = 356.78245.
, то верных цифр в числе 7: a = 356.78245.
Если 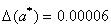 , то верных цифр в числе 8: a = 356.78245.
, то верных цифр в числе 8: a = 356.78245.
------------------------------------------------------------------------------------------------------------
Для оценки погрешностей арифметических операций следует использовать следующие утверждения:
Абсолютная погрешность алгебраической суммы (суммы или разности ) не превосходит суммы абсолютной погрешности слагаемых, т.е.
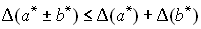
Если а и b - ненулевые числа одного знака, то справедливы неравенства
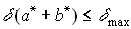 ,
, 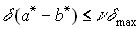 ,
,
где 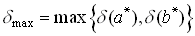 ,
, 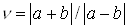
Для относительных погрешностей произведения и частного приближенных чисел верны оценки:
если 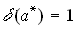 и
и 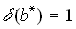 , то
, то 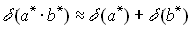 ,
, 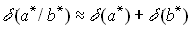 .
.
Пример 4. Погрешности арифметических действий.
Погрешности арифметических действий.
Пусть числа x и y заданы с абсолютными погрешностями  x и
x и  y
y
x : = 2.5378  x : = 0.0001 y : = 2.536
x : = 0.0001 y : = 2.536  y : = 0.001
y : = 0.001
Тогда относительные погрешности чисел
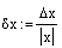 ,
, 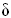 x = 3.94 x 10-5
x = 3.94 x 10-5 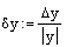 ,
, 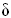 y = 3.94 x 10-4
y = 3.94 x 10-4
Найдем погрешности суммы и разности чисел
S1 : = x + y  S1 : =
S1 : =  x +
x +  y
y 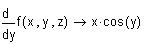
S1 = 5.0738  S1 = 1.1 x 10-3
S1 = 1.1 x 10-3 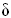 S1 = 2.17 x 10-4
S1 = 2.17 x 10-4
S2 : = x - y  S2 : =
S2 : =  x +
x +  y
y 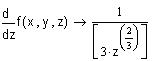
S2 = 1.8 x 10-3  S2 = 1.1 x 10-3
S2 = 1.1 x 10-3 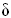 S2 = 0.61
S2 = 0.61
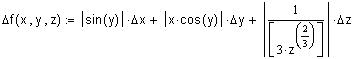
Относительная погрешность разности в 2000 раз больше относительной погрешности суммы!
Возьмем теперь другие значения x и y и вычислим погрешности произведения и частного
x : = 2.5378  x : = 0.0001 y : = 0.006
x : = 0.0001 y : = 0.006  y : = 0.001
y : = 0.001
Тогда относительные погрешности чисел
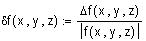
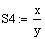
S3 = 0.015227 S4 = 422.966667
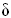 S3 : =
S3 : = 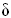 x +
x + 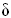 y
y 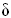 S4 : =
S4 : = 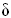 x +
x + 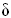 y
y
 S3 : = | S3 | x
S3 : = | S3 | x 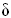 S3
S3  S4 : = | S4 | x
S4 : = | S4 | x 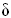 S4
S4
 S3 = 6.604259 x 10-6
S3 = 6.604259 x 10-6  S4 = 0.183452
S4 = 0.183452
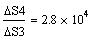
Абсолютная погрешность частного в 20000 раз больше абсолютной погрешности произведения!
------------------------------------------------------------------------------------------------------------
Пусть 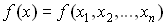 - дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов
- дифференцируемая в области G функция переменных, вычисление которой производится при приближенно заданных значениях аргументов 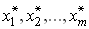 . Тогда для абсолютной погрешности функции
. Тогда для абсолютной погрешности функции  справедлива следующая оценка
справедлива следующая оценка
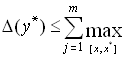
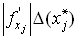 .
.
Здесь [x, x*] v отрезок, соединяющий точки x и x* =( 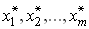 )
)
Для относительной погрешности функции справедливо следующее приближенное равенство
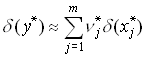 , где
, где 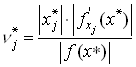
Пример 5. Погрешность вычисления функции.