Хелпикс

Главная

Контакты

Случайная статья



Практическая работа № 12.. Теория.



Практическая работа № 12.

 

Тема: Решение логарифмических уравнений и неравенств.

Цель работы: применение знаний при решении задач.

Теория.

Опр.

Уравнения, содержащие неизвестное под знаком логарифма, называются логарифмическими.

 

Такие уравнения решаются с помощью определения логарифма, теорем о логарифмах и утверждения, что если положительные числа равны, то и равны их логарифмы при данном основании и обратно, если логарифмы чисел равны, то равны и соответствующие им числа. Во всех случаях полученные решения необходимо проверить подстановкой их в данное уравнение и исключить посторонний корень. Часто используется формула перехода от одного основания к другому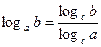

Пример     Решить уравнение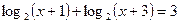

Решение

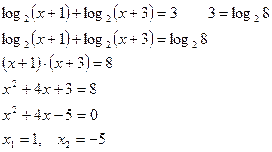
Проверка

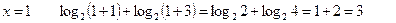- левая часть

                          3=3   х = 1 – корень уравнения

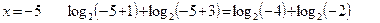- левая часть не имеет смысла

                          х = -5 не является корнем

Ответ: х = 1

                     

При решении простейших логарифмических неравенств типа 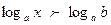необходимо использовать следующее правило:

Если а > 1, то знак неравенства не меняется , т.е. х > b

Если 0 < а < 1, то знак неравенства меняется на противоположный, т.е. х < b.

При решении логарифмических неравенств необходимо проверить, входит ли полученное решение в область определения неравенства.

Пример   Решить неравенство

Решение

                  

Область определения: х + 1 > 0

                                    x > -1  

Общее решение: 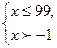  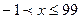                  Ответ: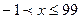

Литература:

1. Ш.А.Алимов «Алгебра и начала анализа» 10-11 кл. , стр. 103 - 108
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.