Тема: Свойства функции: четность, нечетность, периодичность.

Стр 1 из 2Следующая ⇒

Урок

Тема: Свойства функции: четность, нечетность, периодичность.

Задание

1. По конспекту урока ответить на ключевые вопросы темы:

1) Определите понятие четной функции. (Письменно)

2) Определите понятие нечетной функции. (Письменно)

3) Какая функция называется функцией общего вида? (Письменно)

4) Какая функция называется периодической? (Письменно)

5) Назовите наименьшие положительные периоды основных тригонометрических функций. (Письменно)

6) Как найти период функции f (ax +b), где a и b произвольные числа и а≠0?

2. Законспектируйте образцы решения примеров и выполните самостоятельную работу.

Конспект урока

1. Краткая теория

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x).

График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

Функция y = f ( x ) называется периодической,если существует такое число Т >0 , что для каждого х из области определения этой функции значения х+Т и х-Т также принадлежат области определения и выполняется равенство f (x +Т) = f (x). При этом число Т называется периодом функции y = f (x). Отметим, что каждое из чисел nT (n =1, 2, 3,…) также является периодом функции y = f (x).

Если среди положительных периодов функции есть наименьшее число, то его называют наименьшим положительным периодом.

Периодическими, например, являются тригонометрические функции y = sinx, y = cosx, y = tgx, y = ctgx.

Если функция f (х) имеет период Т, то функция f (ax +b), где a и b произвольные числа и а≠0, имеет период, равный .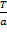

Период функции, представляющей собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.

Число 2π является наименьшим положительным периодом для функций y=sinx и y=cosx.

Число π является наименьшим положительным периодом для функции y=tgx, так как значение тангенса угла поворота будет повторяться через π радиан.

12 Следующая ⇒