
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение заданий.
2.
Вариант 1
Статистическое распределение выборки имеет вид

Тогда значение относительной частоты 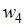 равно …
равно …
· 0,25
· 0,05
· 0,26
· 0,75
Вариант 2.
Статистическое распределение выборки имеет вид

Тогда объем выборки равен …
· 67
· 40
· 5
· 107
Решение заданий.
1. вид
1.
Из генеральной совокупности извлечена выборка объема 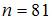 :
:

Тогда значение 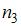 равно …
равно …
· 34
· 81
· 47
· 33
Решение:
Объем выборки вычисляется по формуле 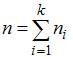 , где
, где 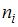 – частота варианты
– частота варианты 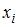 . Тогда
. Тогда 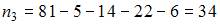 .
.
2.
Из генеральной совокупности извлечена выборка объема 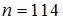 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:
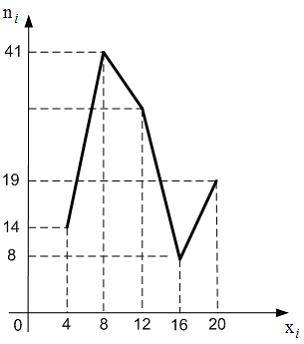
Тогда число вариант 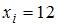 в выборке равно …
в выборке равно …
· 32
· 82
· 8
· 31
Решение:
Объем выборки вычисляется по формуле 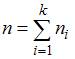 , где
, где 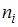 – частота варианты
– частота варианты 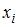 . Тогда
. Тогда 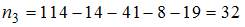 .
.
3.
Из генеральной совокупности извлечена выборка объема 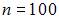 , полигон относительных частот которой имеет вид:
, полигон относительных частот которой имеет вид:
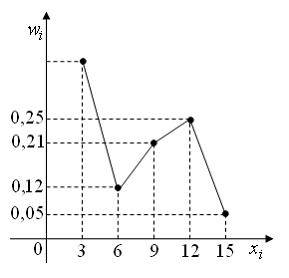
Тогда число вариант 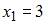 в выборке равно …
в выборке равно …
· 37
· 63
· 100
· 36
Решение:
Вычислим предварительно относительную частоту варианты 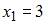 как
как 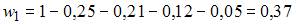 . Тогда из определения относительной частоты
. Тогда из определения относительной частоты 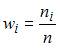 , получаем, что
, получаем, что 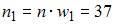 .
.
4.
Из генеральной совокупности извлечена выборка объема 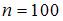 :
:

Тогда относительная частота варианты 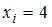 равна …
равна …
· 0,25
· 0,75
· 0,24
· 0,04
………………………………………………………………………………
5.
Из генеральной совокупности извлечена выборка объема 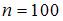 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:
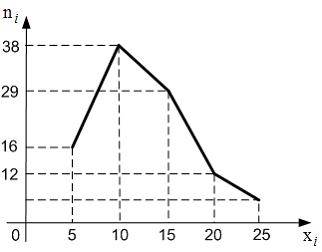
Тогда относительная частота варианты 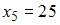 в выборке равна …
в выборке равна …
· 0,05
· 0,06
· 0,25
· 0,20
Решение:
Относительная частота 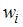 вычисляется по формуле
вычисляется по формуле 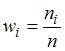 , где
, где 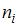 – частота варианты
– частота варианты 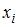 , а
, а 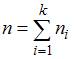 – объем выборки. Вычислим предварительно частоту варианты
– объем выборки. Вычислим предварительно частоту варианты 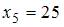 как
как 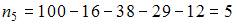 . Тогда
. Тогда 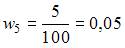 .
.
6.
Из генеральной совокупности извлечена выборка объема 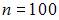 , гистограмма относительных частот которой имеет вид
, гистограмма относительных частот которой имеет вид
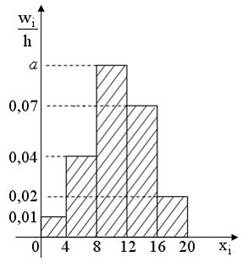
Тогда значение a равно …
· 0,11
· 0,12
· 0,09
· 0,14
Решение:
Так как площадь гистограммы относительных частот равна 1, то 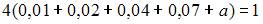 . Тогда
. Тогда 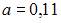 .
.
7.
Из генеральной совокупности извлечена выборка объема 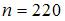 , гистограмма частот которой имеет вид:
, гистограмма частот которой имеет вид:
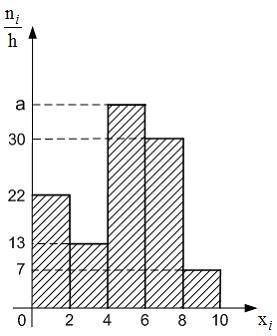
Тогда значение a равно …
· 38
· 39
· 76
· 37
Решение:
Так как объем выборки вычисляется как 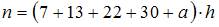 , где
, где 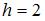 , то
, то 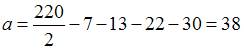 .
.
2.Вид
1.
Статистическое распределение выборки имеет вид

Тогда значение относительной частоты 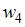 равно …
равно …
· 0,25
· 0,05
· 0,26
· 0,75
Решение:
Сумма относительных частот равна единице. Поэтому 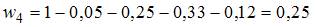 .
.
2.
Статистическое распределение выборки имеет вид

Тогда объем выборки равен …
· 67
· 40
· 5
· 107
Решение:
Объем выборки вычисляется по формуле 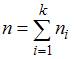 , где
, где 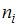 – частота варианты
– частота варианты 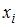 . Тогда
. Тогда 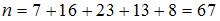 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|