
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1.. В ромбе АВСD угол А равен 60°, сторона ромба равна 4. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DC равно 4. Найти квадрат расстояния от точки А до плоскости ЕDC.
Стереометрия изучает фигуры в пространстве (не все точки фигуры лежат в одной плоскости).
Основными геометрическими фигурами в пространстве являются: точка, прямая и плоскость. Плоскость состоит из точек, неограниченно продолжена во все стороны, не имеет толщины, идеально ровная и гладкая. В пространстве имеется бесконечно много плоскостей, и на каждой из них выполняются свойства планиметрии. Так, например, признаки равенства и подобия треугольников, изученные в планиметрии, справедливы и для треугольников, лежащих в разных плоскостях.
Рассмотрим подробное решение нескольких стереометрических задач.
Задача 1.
Параллельные плоскости α и β пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно.
Найти ВС1, если А1В : А1А1 = 1 : 3, ВС2 = 12. 
Решение.
Рассмотрим рис. 1.
1) Так как А1В : А1А2 = 1 : 3, то А1В = х, А1А2 = 3х.
2) Плоскость (АВС) пересекает плоскость α по прямой А1С1, а плоскость β – по прямой А2С2. Так как плоскости α и β параллельны, то параллельны и прямые А1С1 и А2С2.
3) Рассмотрим угол АВС. По теореме Фалеса выполняется:
ВА1/ВА2 = ВС1/ВС2.
Кроме того, ВА2 = ВА1 + А1А2, а значит, учитывая пункт 1
ВА2 = ВА1 + А1А2 = х + 3х = 4х.
Тогда х/(4х) = ВС₁/12, то есть ВС1 = 3.
Ответ: 3.
Задача 2.
В ромбе АВСD угол А равен 60°, сторона ромба равна 4. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DC равно 4. Найти квадрат расстояния от точки А до плоскости ЕDC.
Решение.
1) Проведем АН перпендикулярно DC (рис. 2), тогда ЕН перпендикулярно DC по теореме о трех перпендикулярах. Значит ЕН – расстояние от точки Е до прямой DC, то есть ЕН = 4.
2) Проведем АК – высоту треугольника АЕН – и докажем, что АК – расстояние от точки А до плоскости (ЕDC):
DC перпендикулярно АН и DC перпендикулярно ЕН, значит, DC перпендикулярно плоскости (АЕН) по признаку перпендикулярности прямой и плоскости. АК содержится в плоскости (АЕН), значит АК перпендикулярно DC. Кроме того, АК перпендикулярна ЕН по построению. Так как прямая АК перпендикулярна двум пересекающимся прямым, лежащим в плоскости ЕDC (ЕН и DC), то АК перпендикулярно плоскости (ЕDC), значит, АК – расстояние от точки А до плоскости (EDC).
3) Рассмотрим треугольник ADH: АD = 4, угол ADH = 60° (накрест лежащий с углом ВАD),
тогда АН = АD · sin ADH. Имеем, что АН = 4 · √3/2 = 2√3.
4) Рассмотрим треугольник ЕАН – прямоугольный (угол ЕАН = 90°). По теореме Пифагора
ЕН2 = ЕА2 + АН2;
ЕА2 = 16 – 12 = 4;
ЕА = 2.
Для площади треугольника ЕАН можно использовать формулы
SEAH = (EA · AH)/2 или SEAH = (AК · ЕH)/2, тогда
EA · AH = AК · ЕH или АК = (EA · AH)/ЕН.
Имеем: АК = (2 · 2√3)/4 = √3, поэтому АК2 = 3.
Ответ: 3. 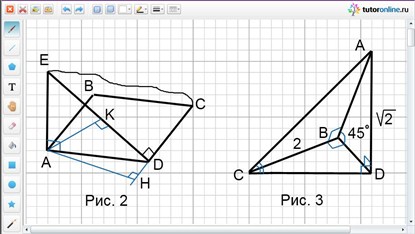
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|