Хелпикс

Главная

Контакты

Случайная статья



Тема: Решение задач.. Формула тонкой линзы, обозначения, единицы измерения.. Решение задач.. Задача 1

Стр 1 из 2Следующая ⇒


Тема: Решение задач.

Дата: 23.10.2020 г.

Студенты должны знать: формулу тонкой линзы, обозначения, единицы измерения.

Студенты должны уметь: применить знания на практике, уметь решать задачи..

План

1. Формула тонкой линзы, обозначения, единицы измерения.

2. Формулы, описывающие свобoдное падение тела по вертикали.

3. Решение задач.

 

1. Формула тонкой линзы, обозначения, единицы измерения.

Формула тонкой линзы связывает между собой три величины:

 

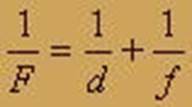
расстояние от предмета до линзы - d

расстояние от линзы до изображения - f

фокусное расстояние линзы - F

 

 

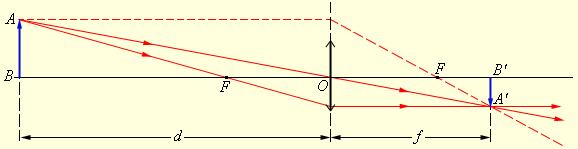
В формуле тонкой линзы фокусное расстояние ОF обозначается буквой F.

- Если линза собирающая, то 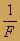 > 0

- Если линза рассеивающая, то перед 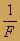 ставится знак «минус»

- Если изображение действительное, то 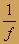 > 0;

- Если изображение воображаемое (мнимое), то перед 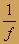 ставится знак «минус».

 

- Все величины в формулу линзы подставляются в метрах.

 

2. Решение задач.

Задача 1

Пред­став­ле­на тон­кая линза, у ко­то­рой ука­за­на глав­ная оп­ти­че­ская ось, и ука­за­но, что в плос­ко­сти, про­хо­дя­щей через двой­ной фокус, рас­по­ла­га­ет­ся све­тя­ща­я­ся точка. Необ­хо­ди­мо опре­де­лить, какая из че­ты­рех точек на чер­те­же со­от­вет­ству­ет пра­виль­но­му изоб­ра­же­нию этого пред­ме­та, то есть све­тя­щей­ся точке.

За­да­ча может быть ре­ше­на несколь­ки­ми спо­со­ба­ми, рас­смот­рим два из них.

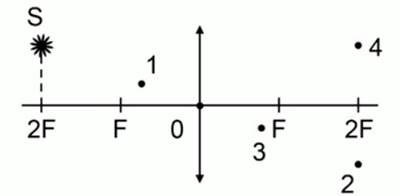
Рис. 1. За­да­ча 1

На рис. 1 изоб­ра­же­на со­би­ра­ю­щая линза с оп­ти­че­ским цен­том (0), фо­ку­сы ( 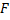), линза раз­но­фо­кус­ная и точки двой­но­го фо­ку­са ( 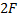). Све­тя­ща­я­ся точка ( 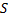) лежит в плос­ко­сти, рас­по­ло­жен­ной в двой­ном фо­ку­се. Необ­хо­ди­мо по­ка­зать, какая из че­ты­рех точек со­от­вет­ству­ет по­стро­е­нию изоб­ра­же­ния или изоб­ра­же­нию этой точки на схеме.

Ре­ше­ние за­да­чи нач­нем с во­про­са по­стро­е­ния изоб­ра­же­ния.

Све­тя­ща­я­ся точка ( 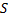) рас­по­ла­га­ет­ся на двой­ном рас­сто­я­нии от линзы, то есть это рас­сто­я­ние равно двой­но­му фо­ку­су, его можно по­стро­ить сле­ду­ю­щим об­ра­зом: взять линию, ко­то­рая со­от­вет­ству­ет лучу, дви­жу­ще­му­ся па­рал­лель­но глав­ной оп­ти­че­ской оси, пре­лом­лен­ный луч прой­дет через фокус ( 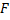), а вто­рой луч прой­дет через оп­ти­че­ский центр (0). Пе­ре­се­че­ние ока­жет­ся на рас­сто­я­нии двой­но­го фо­ку­са ( 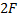) от линзы, это не что иное, как изоб­ра­же­ние, и оно со­от­вет­ству­ет точке 2. Пра­виль­ный ответ: 2.

Од­но­вре­мен­но с этим можно вос­поль­зо­вать­ся фор­му­лой тон­кой линзы и вме­сто 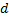под­ста­вить 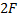, ведь точка лежит на рас­сто­я­нии двой­но­го фо­ку­са, при пре­об­ра­зо­ва­нии по­лу­чим, что изоб­ра­же­ние тоже по­лу­ча­ет­ся в точке, уда­лен­ной на двой­ном фо­ку­се, ответ будет со­от­вет­ство­вать 2 (рис. 2).

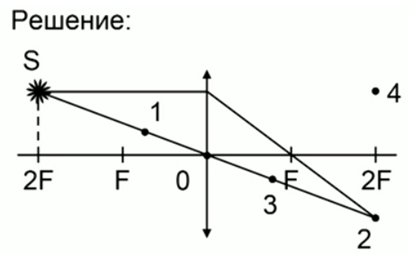
Рис. 2. За­да­ча 1, ре­ше­ние

; ;

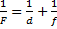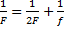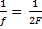
Ответ: 2.

За­да­чу можно было бы ре­шить и с по­мо­щью таб­ли­цы, ко­то­рую мы рас­смат­ри­ва­ли ранее, там ука­за­но, что если пред­мет на­хо­дит­ся на рас­сто­я­нии двой­но­го фо­ку­са, то изоб­ра­же­ние тоже по­лу­чит­ся на рас­сто­я­нии двой­но­го фо­ку­са, то есть, помня таб­ли­цу, ответ можно было бы по­лу­чить сразу.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.