
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Суммативное оценивание за раздел «Первообразная и интеграл»
Суммативное оценивание за раздел «Первообразная и интеграл»
Цель обучения:
11.3.1.1 - знать определение первообразной функции и неопределенного интеграла;
11.3.1.2 - знать и применять свойства неопределенного интеграла;
11.3.1.3 - знать основные неопределённые интегралы
1. 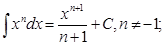
2. 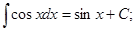
3. 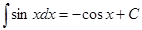 ;
;
4. 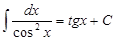 ;
;
5. 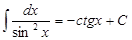 и применять их при решении задач
и применять их при решении задач
11.3.1.4 - знать определение криволинейной трапеции и применять формулу Ньютона-Лейбница для нахождения ее площади;
11.3.1.5 - знать понятие определенного интеграла, уметь вычислять определенный интеграл;
11.3.1.6 - вычислять площадь плоской фигуры, ограниченной заданными линиями;
11.3.1.7 - знать и применять формулу вычисления объема тела вращения с помощью определенного интеграла;
Вариант 1
1.Известно, что 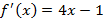 и
и 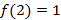 . Найдите:
. Найдите: 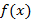
2.Найти неопределенный интеграл:
А) 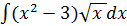 B)
B) 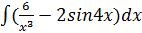
3.Заданы функции: 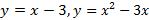
А) изобразите графики заданных функций в одной системе координат
В) найдите координаты точек пересечения графиков заданных функций алгебраическим методом
С) вычислите площадь фигуры, ограниченной полученными линиями
4.Найдите объем фигуры, полученной вращением графика функции: 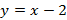 вокруг оси абсцисс, от точки с абсциссой
вокруг оси абсцисс, от точки с абсциссой 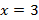 до точки с абсциссой
до точки с абсциссой 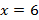
Критерий оценивания
№
задания
Балл
Использует определения первообразной и
неопределенного интеграла
Применяет основные формулы и свойства для нахождения
неопределенного интеграла
2а
2b
Вычисляет площадь плоской фигуры, ограниченной заданными линиями
3а
3b
3с
Вычисляет объем тела вращения с помощью определенного интеграла
Итого: