Тема: Функциональные ряды. Степенные ряды. Ряды Тейлора и Маклорена. Разложение некоторых элементарных функций в степенные ряды. Применение степенных рядов для приближенного вычисления определенных интегралов

Тема: Функциональные ряды

Шилкина, с. 105 – 110.

Выписать определения и формулы для следующих понятий:

на стр. 105 – функциональный ряд, частичная сумма, остаток, область сходимости, сумма функционального ряда; абсолютно сходящийся функциональный ряд.

Степенные ряды

Шилкина, с. 105 – 110.

Выписать определения и формулы для следующих понятий:

на стр. 106 – 107 – степенной ряд; теорема Абеля; интервал, радиус и область сходимости степенного ряда;

на стр. 107. – пример

Ряды Тейлора и Маклорена

Шилкина, с. 105 – 110.

Выписать определения и формулы для следующих понятий:

на стр. 108 – ряд Тейлора, ряд Маклорена, достаточное условие разложения функции в ряд Тейлора, теорема о единственности разложения функции в ряд Тейлора.

Разложение некоторых элементарных функций в степенные ряды

Выписать определения и формулы для следующих понятий:

Шилкина, на стр. 109 – разложение в степенной ряд для экспоненты, синуса, косинуса, двучлена в степени α, натурального логарифма (1 + х);

Марков, на стр. 201 – разложение в степенной ряд для натурального логарифма 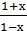, арксинуса, арктангенса.

Применение степенных рядов для приближенного вычисления определенных интегралов

Шилкина, с. 105 – 110.

Пример 4.12 на с. 109 – 110.

Домашнее задание:

1, с. 195 – 202; решить 13.25, 13.28, 13.33; 2, с. 105 – 110.

Литература по теме:

1. Сборник задач и упражнений по высшей математике для студентов экономических специальностей: в 2 ч. / Л.Н.Гайшун, Н.В.Денисенко, А.В.Марков (и др.). – Минск: БГЭУ, 2014. – Ч.2. – 270 с.

2. Шилкина, Е. И. Высшая математика: Часть 2. Учеб.-практ. пособие / Е. И. Шилкина, М. П. Дымков, В. А. Рабцевич. – Мн. : БГЭУ, 2014. – 167 с.