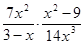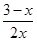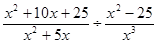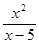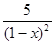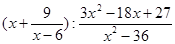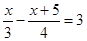Хелпикс

Главная

Контакты

Случайная статья



Алгебраические дроби и действия над ними. Линейные уравнения.



Алгебраические дроби и действия над ними. Линейные уравнения.

Тест №3  

 

1.

Выполните умножение:

Варианты ответов:

      

1)

2) 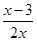3) 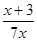4) - 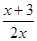5) другой ответ
           

 

2.

Выполните деление:

Варианты ответов:

      

1)

2) - 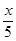3) 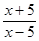4) 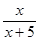5) другой ответ
           

 

3.

Упростите выражение:

Варианты ответов:

      

1)

2) 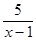3) 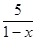4) 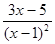5) другой ответ
           

 

4.

Выполните действия:

Варианты ответов:

      

1)

2) 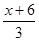3) 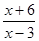4) 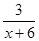5) другой ответ
           

 

 

5.

Какие числа не являются решениями уравнения 7х-0,5=6+1,5(-1-2х)?

Варианты ответов:

      

1) 0,5

 2) - 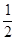3) 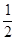4) 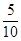5) другой ответ
           

 

6.

Найдите разность корней уравнений: -0,2у-4=0 и 1,9+5у=-2

Варианты ответов:

      

1) 19,12

 2) -19,22 3) -19,12 4) -19,8 5) другой ответ
           

 

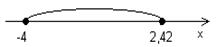
7.

Какому промежутку не принадлежит корень уравнения

2,35(4х-10)=7,2-2(0,3х+3,25)?

Варианты ответов:

      

1)

2)

5) другой ответ

3)

4)
         

 

8.

Решите уравнение: 4(3х-7)-6(х+2)=6х-40

Варианты ответов:

      

1) 6

2) нет решений 3) любое число 4) -6 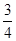5) другой ответ
           

 

9.

Выберите уравнение, которое соответствует условию задачи:

Пешеход сначала шёл в гору со скоростью 3 км/ч, а затем спускался с неё со скоростью 4 км/ч. Найдите путь х, проделанный пешеходом в гору, если дорога в гору на 5 км короче спуска, а на весь путь было затрачено 3 ч.

Варианты ответов:

      

1)

2) 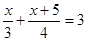3) 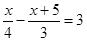4) 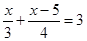5) другой ответ
           

 

10.

Решите задачу:

Моторная лодка прошла 8 ч по течению реки и 6 ч против течения. Определите скорость течения реки, если скорость лодки в стоячей воде 20 км/ч и за все путешествие лодка прошла 290 км.

Варианты ответов:

      

1) 10 км/ч

 2) 5 км/ч 3) 3 км/ч 4) 4 км/ч 5) другой ответ
           

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.