
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Вычисление определителей
Практическая работа №2
Тема: Вычисление определителей
Цель:сформировать умение вычислять определители второго, третьего и n-го порядка.
Теоретические сведения к практической работе
Определение.Определителем (детерминантом) второго порядка называют число, которое ставится в соответствие матрицы второго порядка, и вычисляется следующим образом (обозначается 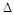 ,
, 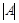 ,
, 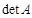 ):
):
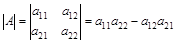 .
.
1) 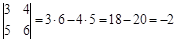 ,
,
2) 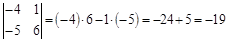 .
.
Определение.Определителем (детерминантом) третьего порядка называют число, которое ставится в соответствие матрицы третьего порядка, и вычисляется по правилу:
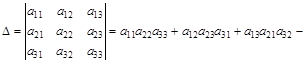
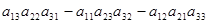
Данный алгоритм называется «правилом треугольника», которое можно представить в виде схемы

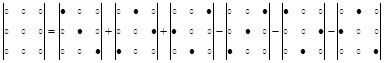
Например, вычислим определитель
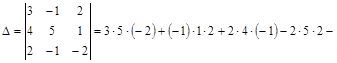
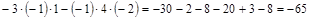 .
.
Для вычисления определителя третьего порядка можно пользоваться алгоритмом Саррюса:
1) После записи определителя дописываем его первый и второй столбец и вычисляем по схеме

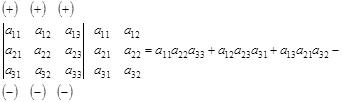
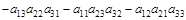 .
.
Например, вычислим определитель по алгоритму Саррюса

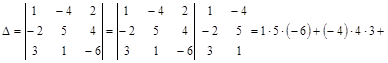
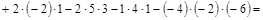
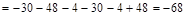 .
.
Определение.Определителем (детерминантом) второго порядка называют число, которое ставится в соответствие матрицы второго порядка, и вычисляется следующим образом Минором элемента 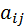 определителя n-го порядка (обозначается
определителя n-го порядка (обозначается 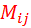 ) называется определитель
) называется определитель 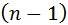 -го порядка, который получают из определителя
-го порядка, который получают из определителя 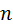 -го порядка вычеркиванием строки и столбца, в которых стоит элемент
-го порядка вычеркиванием строки и столбца, в которых стоит элемент 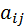 .
.
Например, 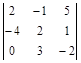
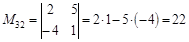 ,
, 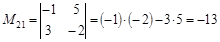 .
.
Определение. Алгебраическим дополнением элемента 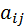 определителя
определителя 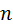 -го порядка (обозначается
-го порядка (обозначается 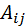 ) называется соответствующий ему минор со знаком
) называется соответствующий ему минор со знаком
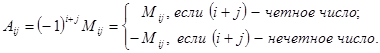
Например, для определителя 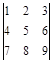
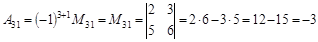 ,
,
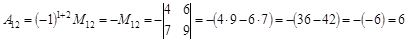 .
.
9) (Теорема Лапласа) Определитель равен сумме произведений элементов некоторого столбца (строки) на соответствующие им алгебраические дополнения.
Например, для определителя третьего порядка
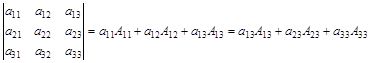 .
.
Пример. 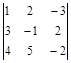
Решение
1) Вычислим определитель.
а) по правилу треугольника.
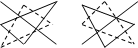
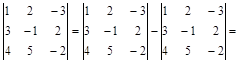
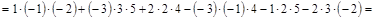
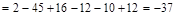 .
.
б) по алгоритму Саррюса.
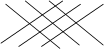
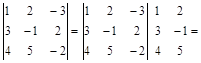
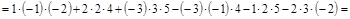
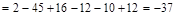 .
.
в) по теореме Лапласа.
Разложим определитель по первому столбцу:
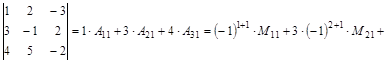
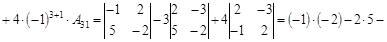

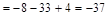 .
.
Содержание практической работы:
Задание. Вычислить определители
1) 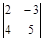 ; 2)
; 2) 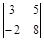 ; 3)
; 3) 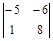 ; 4)
; 4) 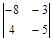 ; 5)
; 5) 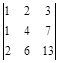 ;
;
6)  ; 7)
; 7) 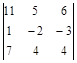 ; 8)
; 8) 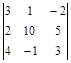 ; 9)
; 9) 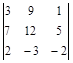 ;
;
10) 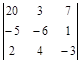 ; 11)
; 11) 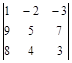 ; 12)
; 12) 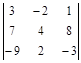 ;
;
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|