Хелпикс

Главная

Контакты

Случайная статья



ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА



ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 5

Наименование предмета:«Техническая механика»

Тема: «Движение несвободной материальной точки»

Наименование работы:«Применение принципа Даламбера к решению задач на прямолинейное движение точки»

Время:90 мин

Цель (обучающая, развивающая, воспитательная):уметь составлять уравнения равновесия для решения задач на прямолинейное движение точки

Форма отчета:тетрадь

Рекомендуемая литература:А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1. Что изучает динамика?

2. Какая система отсчета называется инерциальной?

3. В чем состоит принцип инерции?

4. В чем заключается основной закон динамики?

5. Чему равно значение силы тяжести тела?

Указания к выполнению работы:

1. Повторить по учебнику тему «Движение несвободной материальной точки»

2. Выпишите данные для вашего варианта (согласно нумерации в журнале)

 

№ варианта G, кН F, кН S, м № варианта G, кН F, кН S, м № варианта G, кН F, кН S, м

 

 

3. Рассмотрите пример решения.

Пример. 

 

По наклонной плоскости AB длиной 4 м и углом подъема  ά = 15o равноускоренно поднимают груз M весом  G = 200 кН, постоянной силой F = 65 кН, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз на расстояние AB , если коэффициент трения при движении груза по наклонной плоскости f = 0,05.

Решение.

1. Изобразим тело M на наклонной плоскости с приложенными к нему силами G и F, а также силой трения R f и нормальной реакцией R n наклонной плоскости.

 

 

 

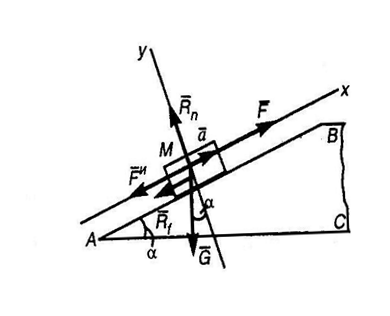
 Находясь под действием этих сил, тело движется по наклонной плоскости с постоянным ускорением  a.

2. Груз перемещается равноускоренно, без начальной скорости. Время его движения можно определить из уравнения движения

S = a t 2 / 2, откуда t = √ 2S/a.

но предварительно необходимо определить ускорение a.

3. Так как груз движется с ускорением, то силы G и F, R f и R n, приложенные к нему, не образуют уравновешенной системы. Приложим к грузу M  силу инерции Fи = ma = Ga / g, направив ее в сторону, противоположную ускорению a. Теперь система пяти

                 
       


сил G, F, R f , R n, F и является уравновешенной.

4. Выберем систему координат, как показано на рис, и спроецируем все силы на оси x и y.  Тогда получим два уравнения равновесия:

             ∑Fkx = 0; F – G sin α - R f - Fи  = 0;                   (1)

                ∑Fky = 0; R n - G cos α = 0.                           (2)

5. Из уравнения (1)

    Fи =  F – G sin α - R f,

но сила трения

R f = f R n .

Нормальную реакцию R n  найдем из уравнения (2)

R n = G  cos α.

Поэтому

Fи = F – G sin α – f G cosα = F- G(sinα + f cosα).

Подставим в это уравнение числовые значения

Fи = 65 – 200 (sin 15o+ 0,05 cos 15o) = 65 - 61,4 = 3,6 кН

6. Из выражения Fи = G/g · а найдем ускорение а:

 

а = (F и · g) /G = (3,6· 9,81) / 200 = 0,18 м / с 2

 

7. Подставив значение ускорения а в выражение t = √2S/2, найдем время перемещения груза М по всей длине наклонной плоскости:

     
 


t = √2 S / а = √2 ·4 / 0,18 = 6,7 с.

4. Решите свой вариант.

5. Ответьте на вопросы.

6. Сделайте вывод.

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.