Хелпикс

Главная

Контакты

Случайная статья



Тема: Логарифмические уравнения и неравенства с параметром

Стр 1 из 2Следующая ⇒


Тема: Логарифмические уравнения и неравенства с параметром

Дата: 05.11.2020 г.

Группа: ПК-261

Студенты должны знать: понятия логарифмической функции, ее свойства, понятия логарифмического уравнения и неравенства, понятие параметра.

Студенты должны уметь:применять основные алгоритмические приемы решения логарифмических уравнений и неравенств, логарифмических уравнений и неравенств с параметром, свойства логарифмов при решении уравнений и неравенств.

1.Актуализация опорных знаний

2.Определение темы урока

 

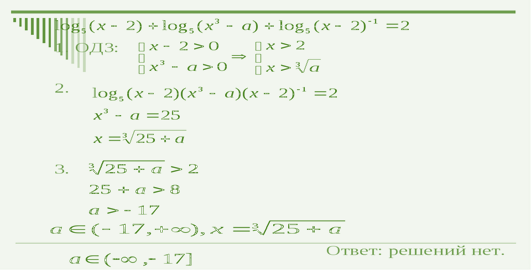
3.Решение упражнений

1)

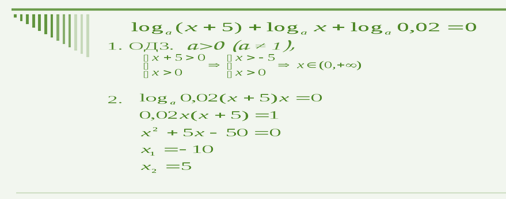2)

3)

4) В зависимости от значений параметра 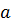 решить уравнение .

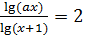Решение.

.

.

, .

 

 

 

 

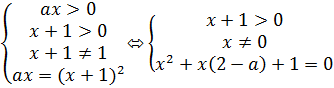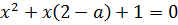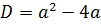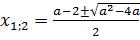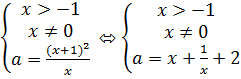
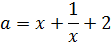
                       0  1                               Х

 

Ответ: 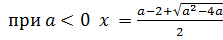, при 0  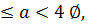при ,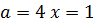

.

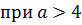
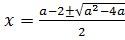5) При каких значениях параметра 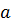 все корни уравнения

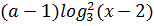 +2( 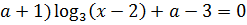 меньше 3?

Область допустимых значений переменной х это 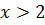. А так как по условию все корни уравнения должны быть меньше 3, т.е.  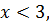то 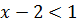. Значит, .

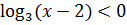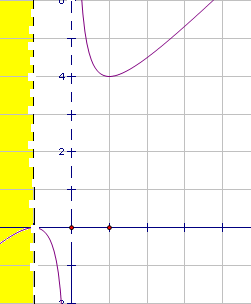
Если обозначить , то уравнение перепишется в виде равносильной системы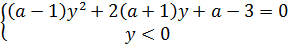

При 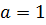 уравнение принимает вид 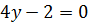, и т. о. 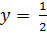. Но это значение  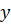противоречит условию .

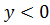Пусть 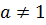. Тогда корни квадратного трехчлена  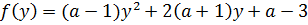будут меньше 0, если совместна система

⬄ ⬄

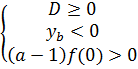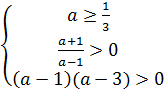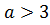
Ответ: .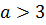

6) При каких значениях параметра 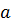уравнение

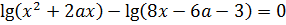 имеет единственное решение.

Решение.

⇔

.

1)

 

⇔ ⇔

2)

 

 

 


⇔

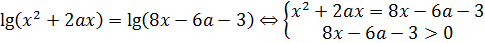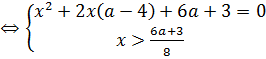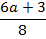
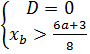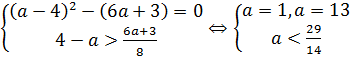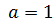
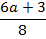
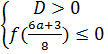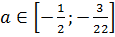
Ответ: .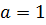

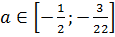
7) При каких значениях параметра 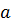 уравнение

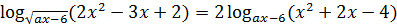 имеет единственное решение?

Решение.

Рассматриваем систему, равносильную данному уравнению

⇔

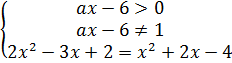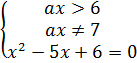
Квадратное уравнение имеет два корня .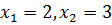

1). ⇔

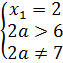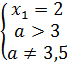
3,5
2). ⇔

 

 

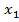
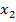
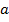
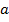
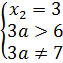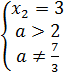
Уравнение имеет единственное решение при 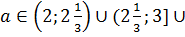{3,5}.

Ответ: 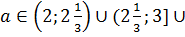{3,5}.

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.