Хелпикс

Главная

Контакты

Случайная статья



Дифференциальное исчисление функции одной переменной



 

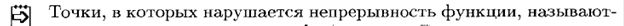
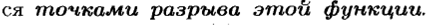
Примеры нарушения условия непрерывности

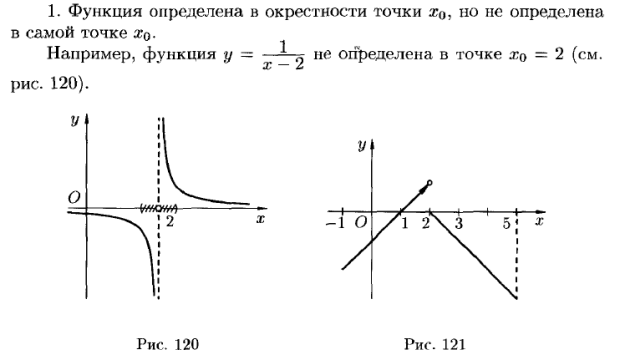
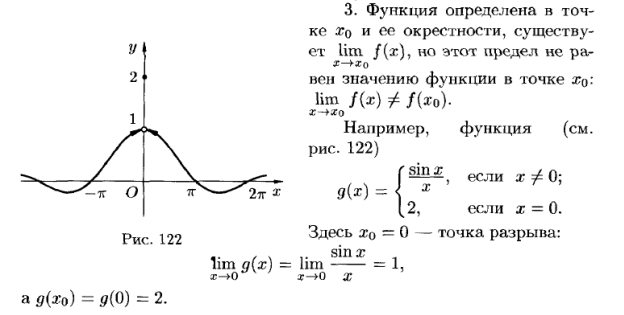
Для функции

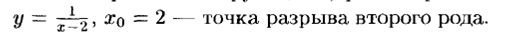
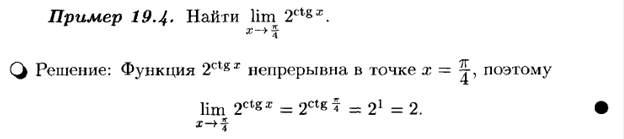
Пример. Рассмотрим функцию 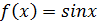. Эта функция непрерывна на отрезке [  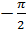, ], где она принимает свое наибольшее значение M = 1 и свое наименьшее значение m = -1.

Пример. Рассмотрим функцию 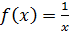. Эта функция непрерывна на промежутке x  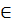(0, 1], где она не ограничена. Здесь условие теоремы 19.4 не выполнено.

Пример. Принимает ли функция 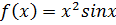 значение 2 на промежутке [ , ] ?

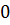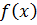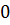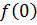Функция  непрерывна на отрезке [ , ] и =0, 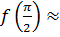 2,91. Так как 0 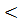2 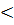 2,91, то по теореме 19.5 существует такая точка x0  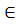( 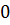, ), где f(x0)=2.

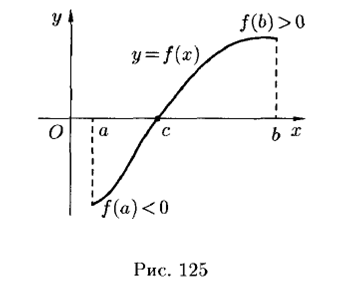
Пример. Доказать, что уравнение x3 + x2 = 1 имеет хотя бы один корень на промежутке (0, 1).

Рассмотрим функцию y(x) = x3 + x2 – 1. Это элементарная функция и она непрерывна на [0, 1]. Находим y(0) = -1, y(1) = 1. Тогда по 19.2 на (0, 1) найдется хотя бы одна точка x = c, где y(c) = 0.

 

Дифференциальное исчисление функции одной переменной

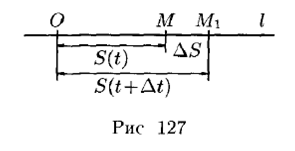
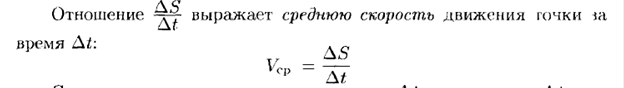
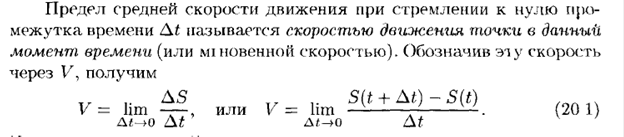
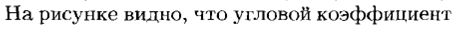
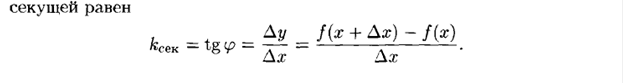
Производная

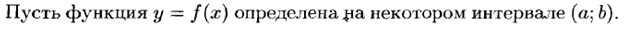
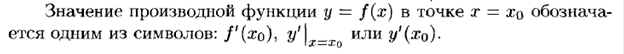
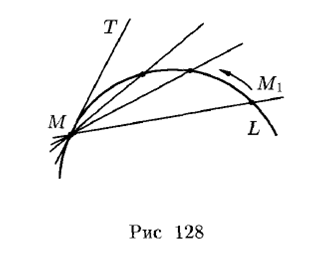
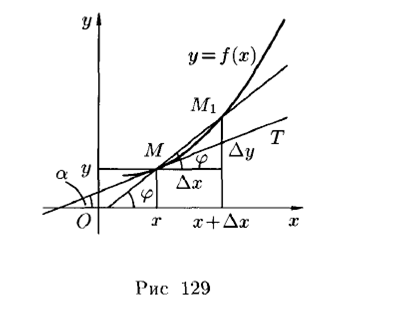
Механический и геометрический смысл производной.

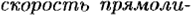
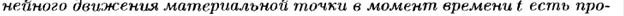
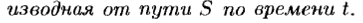
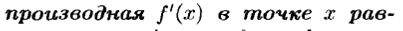
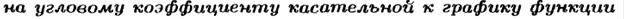
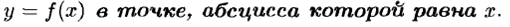
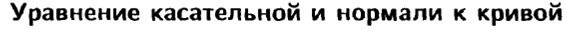
Можно показать, что уравнение касательной к графику функции y= f (x) в точке, абсцисса которой равна x0 имеет вид:

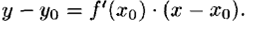
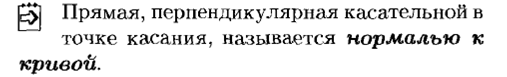
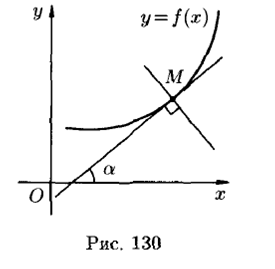
Уравнение нормали имеет вид:

 
  

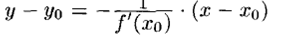
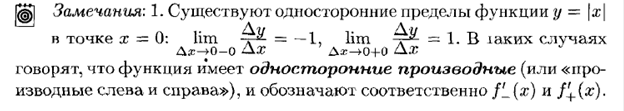
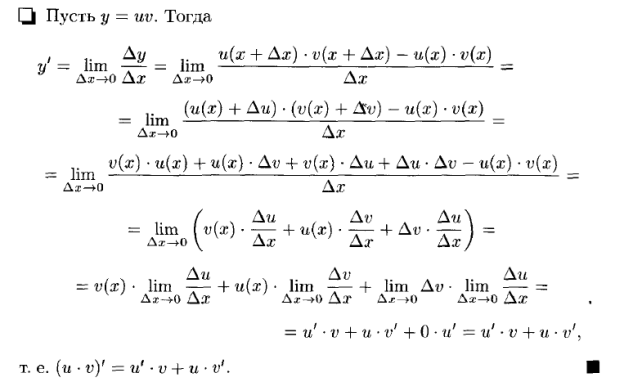
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.