Главная Контакты Случайная статья Автоматизация Антропология Археология Архитектура Биология Ботаника Бухгалтерия Военная наука Генетика География Геология Демография Деревообработка Журналистика Зоология Изобретательство Информатика Искусство История Кинематография Компьютеризация Косметика Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Материаловедение Медицина Менеджмент Металлургия Метрология Механика Музыка Науковедение Образование Охрана Труда Педагогика Полиграфия Политология Право Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Электротехника Энергетика
	Дисциплина «Математика (алгебра, начала математического анализа, геометрия)» Стр 1 из 2Следующая ⇒   03.11.2020г.     1ТПС-6-20         Дисциплина «Математика (алгебра, начала математического анализа, геометрия)»
Занятие №24
Преподаватель Садовая Е.В.
Тема занятия: Тождественные преобразования логарифмических выражений
Вид занятия: лекция
Цель дидактическая: закрепить и проверить навыки применения свойств логарифмов к преобразованию логарифмических выражений; продолжить формирование у студентов умений применять свойства степеней, корней и свойства логарифмов при решении упражнений на преобразование выражений.

Учебник:Алгебра и начала математического анализа,10-11. Ш. А. Алимов, Ю. М. Колягин и др., Просвещение, 2014.

Ход занятия

I. Повторение теоретических сведений (законспектировать файлы презентации)

Вопросы:

1.Определение логарифма:                     2. Основное логарифмическое тождество:

3. Натуральный и десятичный логарифмы:                4. Свойства логарифмов:

II. Объяснение нового материала.

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.

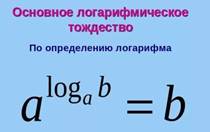
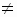Пусть а>0, а 1, в›0, с>0, r– любое действительное число. Тогда справедливы формулы:

1. log_а (вс) = log_а в + log_а с;

2. log_а (в/с) = log_а в – log_{а с;}

3. log_а в ^r = r log_а в.

Рассмотрим примеры :

а) log₆ 18 + log₆ 2 = log₆ 18*2 = log₆ 36=2
б) log₁₂ 48 – log₁₂ 4 = log₁₂ 48/4 = log₁₂ 12 = 1
в) log₃ 3 ^1/4 = ¼ log₃ 3 = 1*¼ = ¼

 3. Решение задач (выполнить в конспекте)

1) log₁₀5 + log₁₀ 2 =
2) log₁₂ 2 + log₁₂ 72 =

3) log₂15 – log₂ 15/16 =
4) log_1/3 54 – log_1/3 2 =

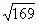5) log₁₃ = log₁₃ 169^1/5 .
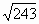6) log_1/3 = log_1/3 243^1/4

7) log₈ 12 – log₈ 15 + log₈ 20 =

а) log₃6 + log₃ 3/2 =

б) log₈ 1/16 – log₈ 32 =