Связь между давлением и средней кинетической энергией теплового движения молекул идеального газа

Связь между давлением и средней кинетической энергией теплового движения молекул идеального газа

Большое число молекул газа и хаотичность их движения приводит к тому, что все направления их движения встречаются одинаково часто. Соударения между частицами приводят к непрерывному изменению их скоростей. Поэтому для описания движения одной частицы можно использовать законы Ньютона, а для описания движения большого числа частиц эти законы использовать нельзя. Для описания поведения большого числа частиц используют теорию вероятностей, с помощью которой находят средние значения физических величин – среднее значение скорости частицы v, среднее значение кинетической энергии частицы E.

Основное уравнение МКТ устанавливает связь между макропараметром – давлением и микропараметрами, характеризующими частицу. Давление идеального газа пропорционально произведению массы молекулы на концентрацию молекул и средний квадрат их скорости:

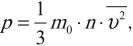
где m0 – масса частицы, n – концентрация частиц, v2¯¯¯¯¯ – среднее значение квадрата скорости.

Среднее значение квадрата скорости находится по формуле:

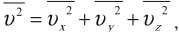
где v2x¯¯¯¯¯,v2y¯¯¯¯¯,v2z¯¯¯¯¯ – средние значения квадрата проекции скорости на оси ОХ, ОУ и ОZ соответственно.

Среднее значение квадрата проекции скорости на оси ОХ вычисляется по формуле:

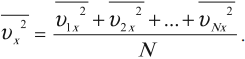
Аналогично вычисляются средние значения квадрата проекции скорости на оси ОУ и ОZ.

Так как все направления движения из-за хаотичности движения молекул равновероятны, то:

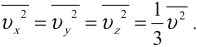
Множитель 13 появляется вследствие существования трех проекций у любого вектора скорости.

Важно!
При решении задач не путать среднее значение квадрата скорости и среднюю квадратичную скорость vск=v2¯¯¯¯¯−−√ (м/с). Единица измерения в СИ среднего значения квадрата скорости – м²/с².

Средняя кинетическая энергия поступательного движения молекулы:

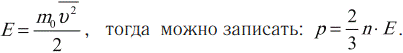
Давление идеального газа пропорционально концентрации молекул и средней кинетической энергии их поступательного движения.