Второй этап всероссийской олимпиады школьников по математике

Второй этап всероссийской олимпиады школьников по математике

2015-2016 учебный год

9 класс (задания)

1. Докажите, что число 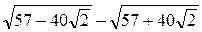является целым и найдите его.

2. Не решая уравнение 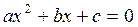, составьте уравнение второй степени, корни которого были бы четвёртыми степенями корней данного уравнения.

3. Докажите, что уравнение 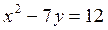не имеет решений в целых числах.

4. На плоскости произвольным образом расположены 2015 точек, не лежащих на одной прямой. Докажите, что при любом расположении точек можно найти ломаную линию без самопересечений с вершинами в этих точках.

5. В клетках квадрата 10˟10 расставлены попарно различные целые числа. Докажите, что есть пара клеток с обшей стороной, числа в которых отличаются не менее, чем на 6.