
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема. Разложение вектора по направлениям
Занятие по математике №30 Группа 2ЖЗ Дата проведения: 30.10.20г.
Тема. Разложение вектора по направлениям
Видеоурок по данной теме просмотреть по ссылке: https://www.youtube.com/watch?v=28tsaYte3W0
Материал занятия для самостоятельного изучения.
Аналогично тому, как на плоскости любой вектор можно разложить по двум неколлинеарным векторам, наверняка, в пространстве любой вектор можно разложить по трём некомпланарным векторам.
Говорят, что вектор 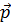 разложен по векторам
разложен по векторам 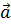 ,
, 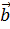 ,
, 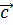 если он представлен в виде суммы произведений вектора
если он представлен в виде суммы произведений вектора 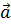 на число x, вектора
на число x, вектора 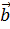 на число y и вектора
на число y и вектора 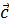 на число z.
на число z.
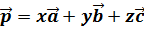
При этом числа x, y и z называют коэффициентами разложения.
Запишем теорему. Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Докажем эту теорему для некомпланарных векторов 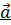 ,
, 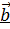 ,
, 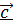 .
.
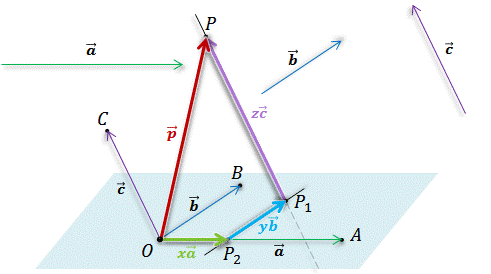
Отметим любую удобную точку пространства и отложим от неё векторы 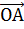 ,
, 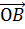 ,
, 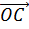 и
и 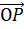 равные векторам
равные векторам 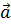 ,
, 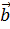 ,
, 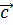 соответственно.
соответственно.
Далее через точку P проведём прямую параллельную прямой OC. Точку пересечения этой прямой с плоскостью ABC обозначим за P1.
Далее через точку P1 проведём прямую параллельную прямой OB. А точку пересечения этой прямой с прямой ОА обозначим за P2.
Пользуясь правилом многоугольника сложения нескольких векторов, запишем, что 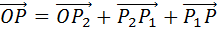 .
.
Из построений следует, 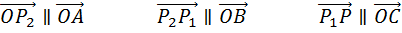 . А это значит, что
. А это значит, что 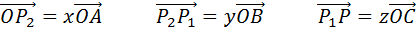 .
.
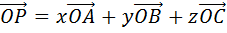
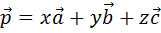 .
.
Таким образом мы разложили вектор 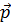 по трём некомпланарным векторам
по трём некомпланарным векторам 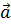 ,
, 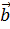 ,
, 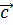 .
.
Осталось только доказать, что коэффициенты разложения x, y, z определяются единственным образом.
Допустим, что кроме полученного нами разложения есть ещё одно, в котором коэффициенты разложения равны x1, y1, z1.
Вычтем второе разложение из первого.
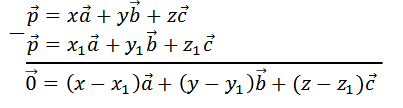
Понятно, что в разложении нулевого вектора по трём некомпланарным ненулевым векторам все коэффициенты разложения должны быть равны нулю.
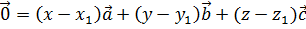
Отсюда соответственно равны коэффициенты:
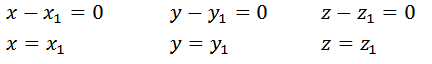
А это противоречит нашему допущению о том, что коэффициенты второго разложения вектора 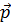 отличны от коэффициентов первого разложения.
отличны от коэффициентов первого разложения.
Отсюда получаем, что коэффициенты разложения x, y, z определяются единственным образом.
Что и требовалось доказать.
Выполним несколько заданий.
Задача 1. 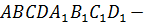 параллелепипед.
параллелепипед.
Разложить:
а) вектор 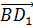 по векторам
по векторам 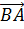 ,
, 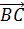 и
и 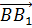 ;
;
б) вектор 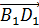 по векторам
по векторам 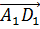 ,
, 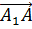 и
и 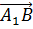 .
.
Решение.
Изобразим все векторы, перечисленные в первом пункте. Пользуясь правилом параллелепипеда сложения трёх некомпланарных векторов, нетрудно заметить, что 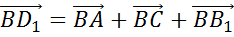 . Таким образом мы разложили вектор
. Таким образом мы разложили вектор 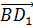 по данным векторам. Причём каждый коэффициент данного разложения равен единице.
по данным векторам. Причём каждый коэффициент данного разложения равен единице.
Обратимся к следующему пункту. Вектор 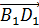 нужно разложить по векторам
нужно разложить по векторам 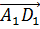 ,
, 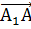 и
и 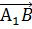 .
.
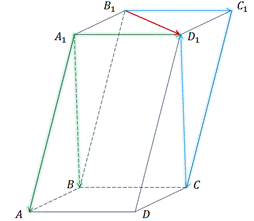
Для начала запишем, что по правилу многоугольника сложения нескольких векторов, вектор 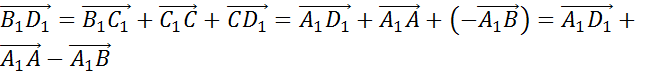 .
.
Так мы разложили вектор 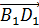 по данным векторам, где коэффициенты разложения y и x равны 1, а z равно -1.
по данным векторам, где коэффициенты разложения y и x равны 1, а z равно -1.
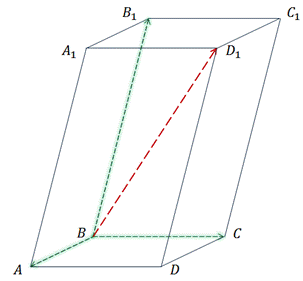
Задача 2. 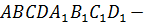 параллелепипед.
параллелепипед. 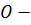 точка пересечения диагоналей. Разложить векторы
точка пересечения диагоналей. Разложить векторы 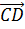 и
и 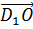 по векторам
по векторам 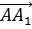 ,
, 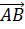 и
и 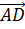 .
.
Решение.
Сразу можно отметить, что 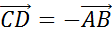 .
.
Поэтому в разложении этого вектора по данным векторам коэффициенты разложения при векторах 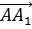 и
и 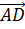 равны 0, а при векторе
равны 0, а при векторе 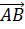 — -1.
— -1.
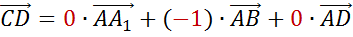
Далее разложим вектор 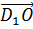 по данным векторам.
по данным векторам.
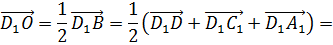
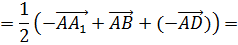
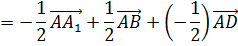
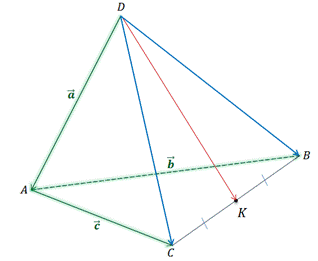
Задача 3. 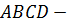 тетраэдр.
тетраэдр. 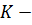 середина ребра
середина ребра 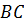 . Разложить векторы
. Разложить векторы 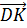 по векторам
по векторам 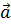 ,
, 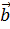 и
и 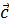 . Если
. Если 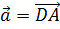 ,
, 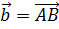 и
и 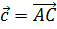 .
.
Решение.
Для начала стоит отметить, что на рёбрах DC и DB тетраэдра можно построить параллелограмм. И отрезок DK будет являться половиной его диагонали DD1. Действительно, точка К является серединой второй диагонали BC, а значит, она является точкой пересечения диагоналей данного параллелограмма.
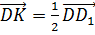
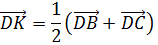
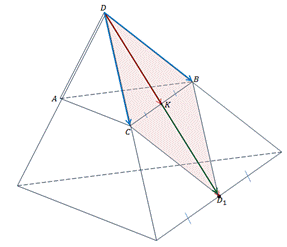
Рассмотрим каждый вектор этой суммы в отдельности.
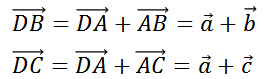
Подставим полученные суммы в выражение для вектора 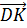 .
.
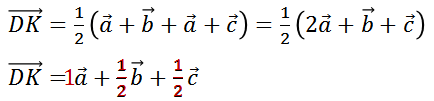
Домашнее задание:повторить §1, п.46-48, «Геометрия 10-11 класс» Л.С. Атанасян, составить краткий конспект занятия, рассмотреть и записать решение задач 1-3.
Выполненные задания отправлять на электронную почту: tatiefremenko@yandex.ua
или страницу вКОНТАКТЕ - https://vk.com/id592773352
Индивидуальные консультации, оценивание устных ответов по тел.: 0660627421, 0721813966 Ефременко Т.А.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|