ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ


Дата	20.10.2020
Группа	150-1
Дисциплина	Информатика
Форма занятия	Лекция (конференция ZOOM)
Тема	Арифметические основы работы компьютера
Форма обратной связи	Файл выполненной работы прикрепить https://vk.com/topic-193118586_46380099
Сроки выполнения	В течение дня

1.Изучить презентацию и краткий теоретический материал, представленный ниже.

2.Выполнить задание

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным правилам.

Правила выполнения арифметических операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление уголком. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Таблицы сложения в любой позиционной системе счисления легко составить, используя правило счета:

Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.

Таблица сложения в двоичной системе:

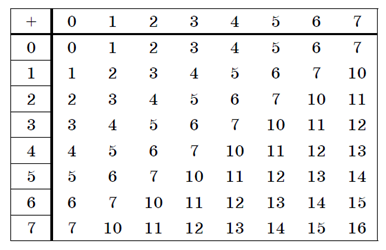Таблица сложения в восьмеричной системе:

Пример:

1) Сложим числа 15 и 6 в различных системах счисления.

Решение. Переведем числа 15 и 6в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения (см. выше).

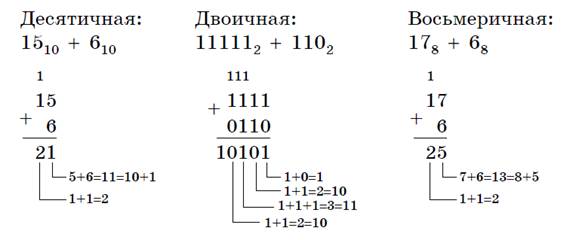
Ответ: 15+6=2110=101012=258

2) Вычислим сумму чисел 438 и 5616. Результат представим в восьмеричной системе счисления.

Решение: переведем число 5616 в восьмеричную систему счисления, используя поразрядный способ перевода разложением на тэтрады и триады:

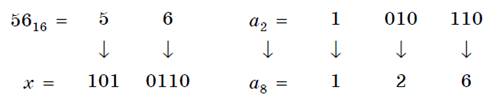
Пользуясь правилами сложения в восьмеричной системе счисления, получаем:

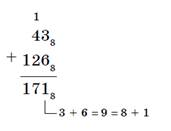
Ответ: 438 + 5616 = 1718

Вычитание осуществляется по тем же правилам, что и в десятичной системе счисления.

При вычитании из меньшего числа большего производится заем из старшего разряда.

Пример:

Вычислим разность X−Y двоичных чисел, если X=10101002 и Y=10000102. Результат представим в двоичном виде.

Решение:

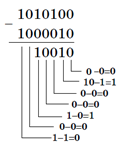
Ответ: 100102

Замечание. Если вам трудно складывать или вычитать в системах счисления, отличных от десятичной, можете перевести числа в десятичную систему счисления, выполнить арифметические действия, а затем результат перевести в требуемую в ответе систему счисления.

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Таблица умножения в двоичной системе:

Таблица умножения в восьмеричной системе:

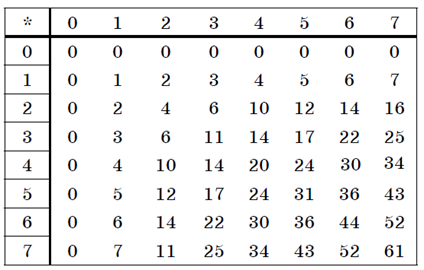
Умножение многоразрядных чисел в различных позиционных системах счисления происходит по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.

Пример:

Перемножим числа 15 и 12.

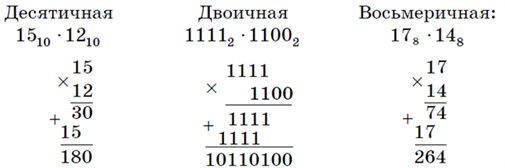
Ответ: 15⋅12=18010=101101002=2648

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. Следует только грамотно пользоваться теми цифрами, которые входят в алфавит используемой системы счисления.

Обрати внимание!

При выполнении любых арифметических операций над числами, представленными в разных системах счисления, следует предварительно перевести их в одну и ту же систему.