Контакты

Случайная статья

Тема: Решение уравнений высокого порядка

ИС1-20-ОТ – 03.11.2020

Тема: Решение уравнений высокого порядка

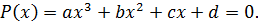
Теорема Безу (следствие). Если 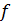– корень многочлена 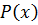, то он делится на 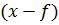без остатка.

Теорема. Каждый рациональный корень 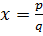, где 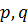– взаимно простые числа, удовлетворяет условию:

а) 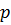– делитель свободного члена ,

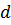б) 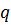– делитель старшего коэффициента .

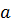Задача № 1. Решить кубическое уравнение .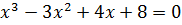

Замечание. +-3 в списке делителей выписаны ошибочно.

Задача № 2. Решить уравнение четвертой степени

Задача № 3. Решить уравнение самостоятельно

.

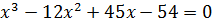1. Делители (-54): +-1; +-2; +-3; +-6; +-18; +-54

+-1 – не подходит, т.к. многочлен не обращается в 0;

3 – подходит

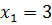– корень уравнения.

Остальные корни находим делением 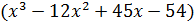на 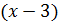столбиком. Получим неполное частное 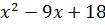. Его корни, по теореме Виета, равны

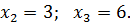
Ответ: 3; 6

Задача № 4. Упростить выражение

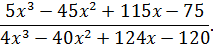
смотрите ниже

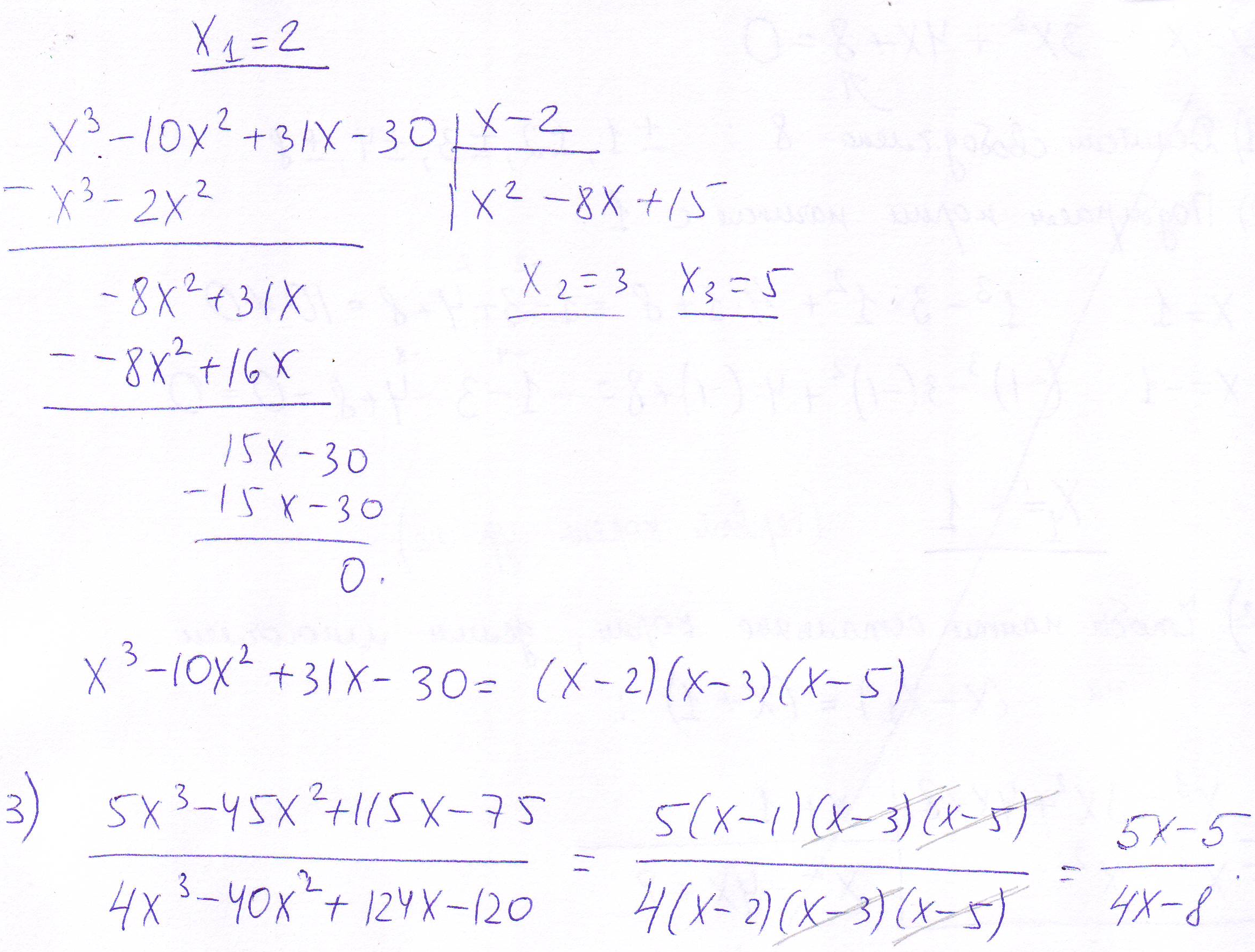
Задача № 5. Решить неполное кубическое уравнение .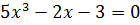

Для самостоятельного разбора. Не забыть добавить в многочлен младшие степени, входящие с нулевым коэффициентом.

Ответ: 1.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.