Правила Лопиталя для раскрытия неопределенностей при вычислении пределов функций.

12. Правила Лопиталя для раскрытия неопределенностей при вычислении пределов функций.

Дифференциальное исчисление значительно облегчает задачу раскрытия неопределенностей при вычислении пределов. Простой прием раскрытия неопределенностей вида и дает правило Лопиталя, сущность которого заключается в следующей теореме.

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций при равен пределу отношения их производных, если последний существует, то есть ( может быть конечным и бесконечным).

Пример 1. Найти .

Решение. Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при 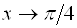являются бесконечно малыми, то есть имеем неопределенность вида , следовательно можно воспользоваться правилом Лопиталя:

Пример 2. Найти .

Решение. .

Правило Лопиталя можно применять неоднократно, если отношение производных снова дает неопределенность или .

Пример 3. Найти .

Решение.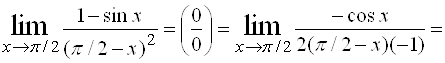

Замечание 1. Применяя неоднократно правило Лопиталя, нужно каждый раз проверять, не раскрылась ли уже неопределенность, иначе можно получить неверный результат.

Замечание 2. В теореме требование существования является существенным, так как если он не существует, то это не означает, что тоже не существует. Например, – не существует, однако .

12 Следующая ⇒