Графическая работа №4 на тему: «Построение проекций геометрических тел».

02.11.2020г.

Графическая работа №4 на тему: «Построение проекций геометрических тел».

Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.

Для выполнения и чтения чертежей деталей нужно знать, как изображаются геометрические тела.

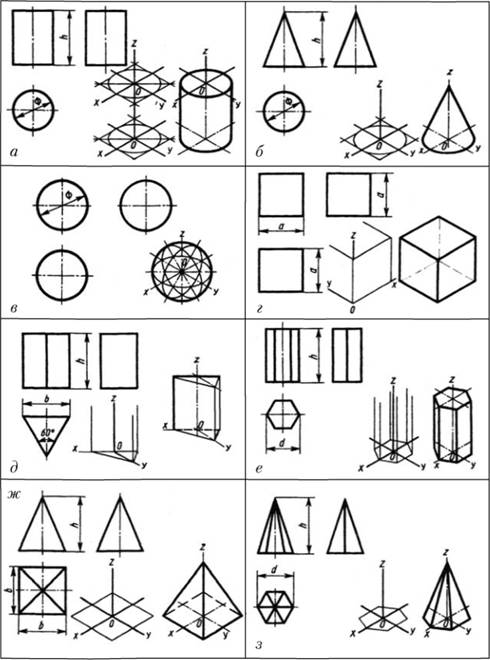
Рисунок 1 - Проекции геометрических тел

Построение проекций прямого цилиндра с вертикальной осью (рис. 1, а) начинают с изображения основания цилиндра, представляющего собой круг. Поскольку круг расположен параллельно плоскости проекций π1 и, следовательно, изображается на ней без искажений, его горизонтальная проекция – круг, а фронтальная и профильная – горизонтальные отрезки прямых, равные диаметру круга. Фронтальная и профильная проекции цилиндра очерчиваются отрезками прямых, представляющими проекции его основания и крайних образующих. На всех проекциях проводят оси симметрии. Размеры цилиндра определяются диаметром его основания и высотой.

Фронтальная и профильные проекции цилиндра одинаковы, поэтому в данном случае профильная проекция лишняя. На рис. 1 чертежи всех геометрических тел выполнены в трех проекциях лишь с той целью, чтобы показать, какие проекции эти тела имеют.

Одно изображение конуса вращения (рис. 1, б) сходно с изображением цилиндра. Так, на горизонтальной проекции конус изображен кругом. На нем наносят центровые линии. Диаметр круга равен диаметру основания конуса. Два других изображения конуса – равнобедренные треугольники. На этих проекциях также наносят оси симметрии. Для конуса указывают диаметр его основания и высоту.

На рис. 1, в представлены чертеж и наглядное изображение шара. Все проекции шара – окружности. Диаметр их равен диаметру шара. На каждом изображении проводят центровые линии.

Так же как и шар, куб имеет три одинаковые проекции (рис. 1, г). Все грани его – квадраты. Размеры куба определяют три измерения: длину, ширину и высоту, равные между собой.

Построение изображений правильной треугольной призмы (рис. 1, д) следует начинать с основания – равностороннего треугольника. На фронтальной плоскости проекций задняя грань призмы изображается в натуральную величину, две передние – с искажением ширины. На профильной проекции ширина прямоугольника равна высоте фигуры основания призмы. На горизонтальной и фронтальной проекциях проводят осевые линии, на профильной проекции ось симметрии отсутствует. Для правильной треугольной призмы указывают ее высоту, длину стороны основания и угол.

Построение прямоугольных проекций правильной шестиугольной призмы (рис. 1, е) также начинают с вычерчивания вида сверху, который представляет собой правильный шестиугольник. На главном виде средняя грань изображается в натуральную величину, а ширина боковых граней искажена. На профильной проекции грани изображаются искаженными по ширине. Размеры правильной шестиугольной призмы определяют ее высотой и шириной, равной удвоенной длине стороны основания.

На рис. 1, ж приведены три проекции и наглядное изображение правильной четырехугольной пирамиды. Основание ее, параллельное горизонтальной плоскости проекций, проецируется на нее в натуральную величину, т.е. изображается квадратом. Боковые ребра, идущие из вершин основания к вершине пирамиды, изображаются диагоналями. Фронтальная и профильная проекции представляют собой равнобедренные треугольники, высота которых равна высоте пирамиды. На всех проекциях должны быть нанесены оси симметрии. Для правильной четырехугольной пирамиды указывают длины двух сторон основания и высоту.

Аналогичны изображения правильной шестиугольной пирамиды (рис. 1, з). Горизонтальной проекцией ее является правильный шестиугольник с диагоналями, изображающими боковые ребра пирамиды. На фронтальной проекции видны три грани, а на профильной – две. На всех проекциях проводят оси симметрии. Размеры правильной шестиугольной пирамиды определяются ее высотой и шириной, равной удвоенной длине стороны основания.

12 Следующая ⇒