
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Нижегородский государственный архитектурно-строительный университет»
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Нижегородский государственный архитектурно-строительный университет»
Инженерно-строительный факультет
Кафедра теории сооружений и технической механики
Расчётно-графическая работа №1
по дисциплине «Сопротивление материалов»
на тему:
ГЕОМЕТРИЧЕСКАЯ ХАРАКТЕРИСТИКА СЕЧЕНИЙ
Выполнил студент гр.157 Пестряков А.А.
Руководитель Шкода И.В.
Нижний Новгород
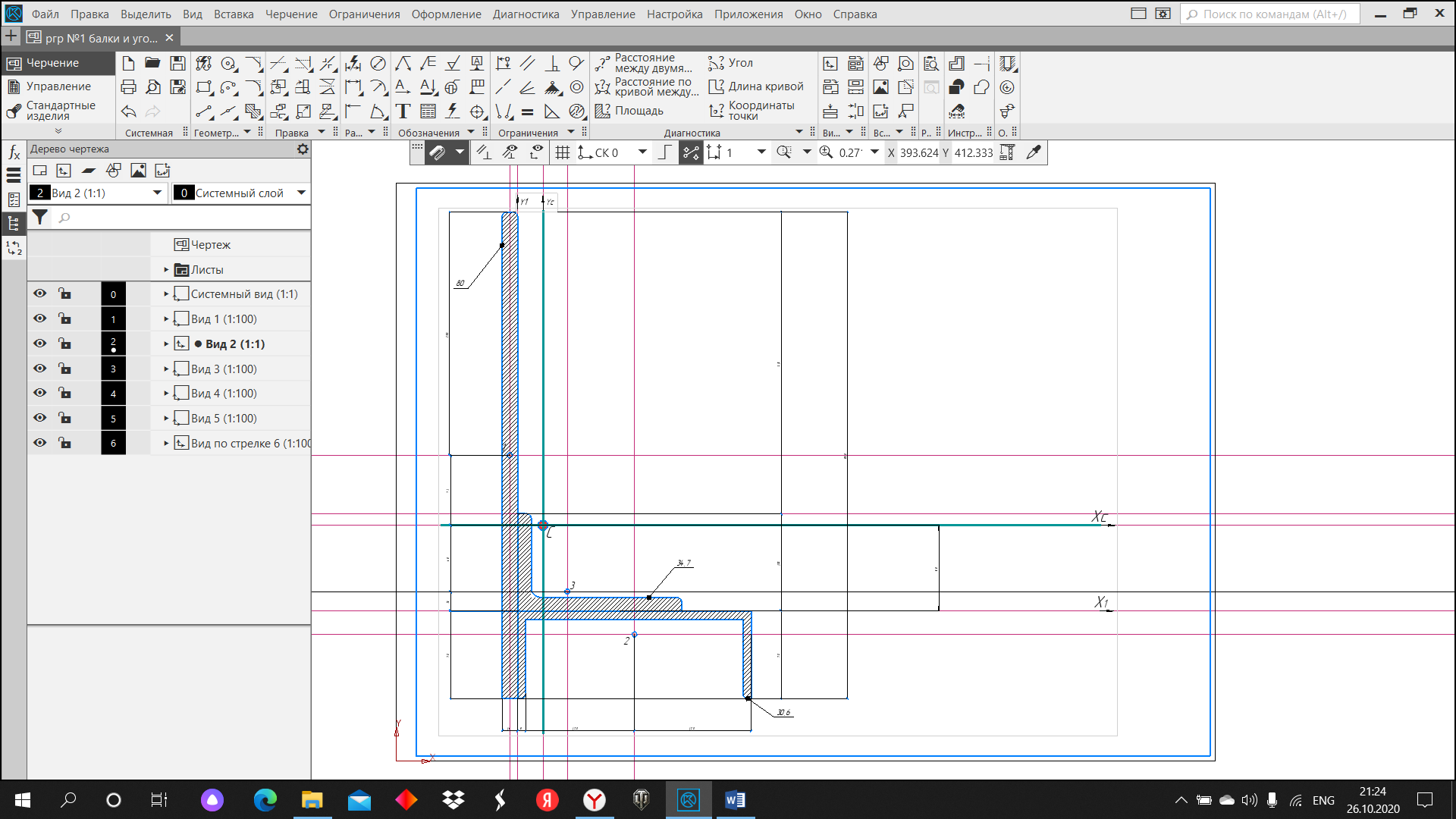
Пример 1. Для заданного поперечного сечения стального стержня, состоящего из следующих элементов:
1. вертикального листа 500 х 16 мм;
2. прокатного швеллера № 24;
3. неравнополочного уголка 160 х 100 х 14 мм,
необходимо определить:
- положение центра тяжести поперечного сечения (т. С);
- главные центральные оси поперечного сечения;
- главные центральные моменты инерции поперечного сечения;
- главные центральные радиусы инерции сечения.
Р е ш е н и е.
Геометрические характеристики элементов, составляющих заданное сечение:
| № эл-та | Элементы | Площадь в см2 Аi | Моменты инерции сечения элементов в см4 | ||

| 
| 
| |||
| 1. | Вертикальный лист 500х16 | А1 = 80 |  =16667 =16667
|  =0 =0
|  = 0 = 0
|
| 2. | Уголок 160x100x14 | А2 = 34,7 |  = 272 = 272
| 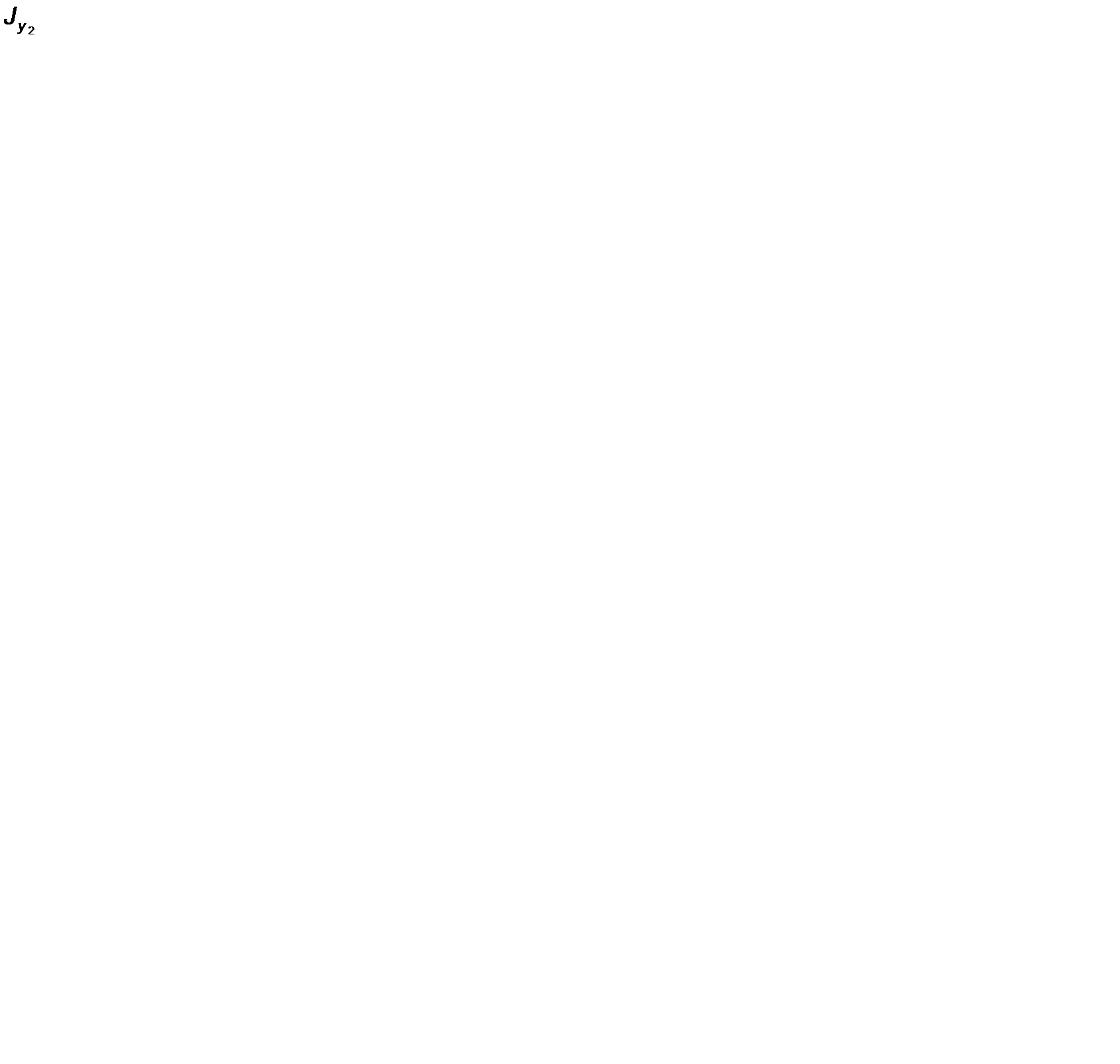 = 897 = 897
|  = 0 = 0
|
| 3. | Швеллер № 24 | А3 = 30,6 |  = 208 = 208
| 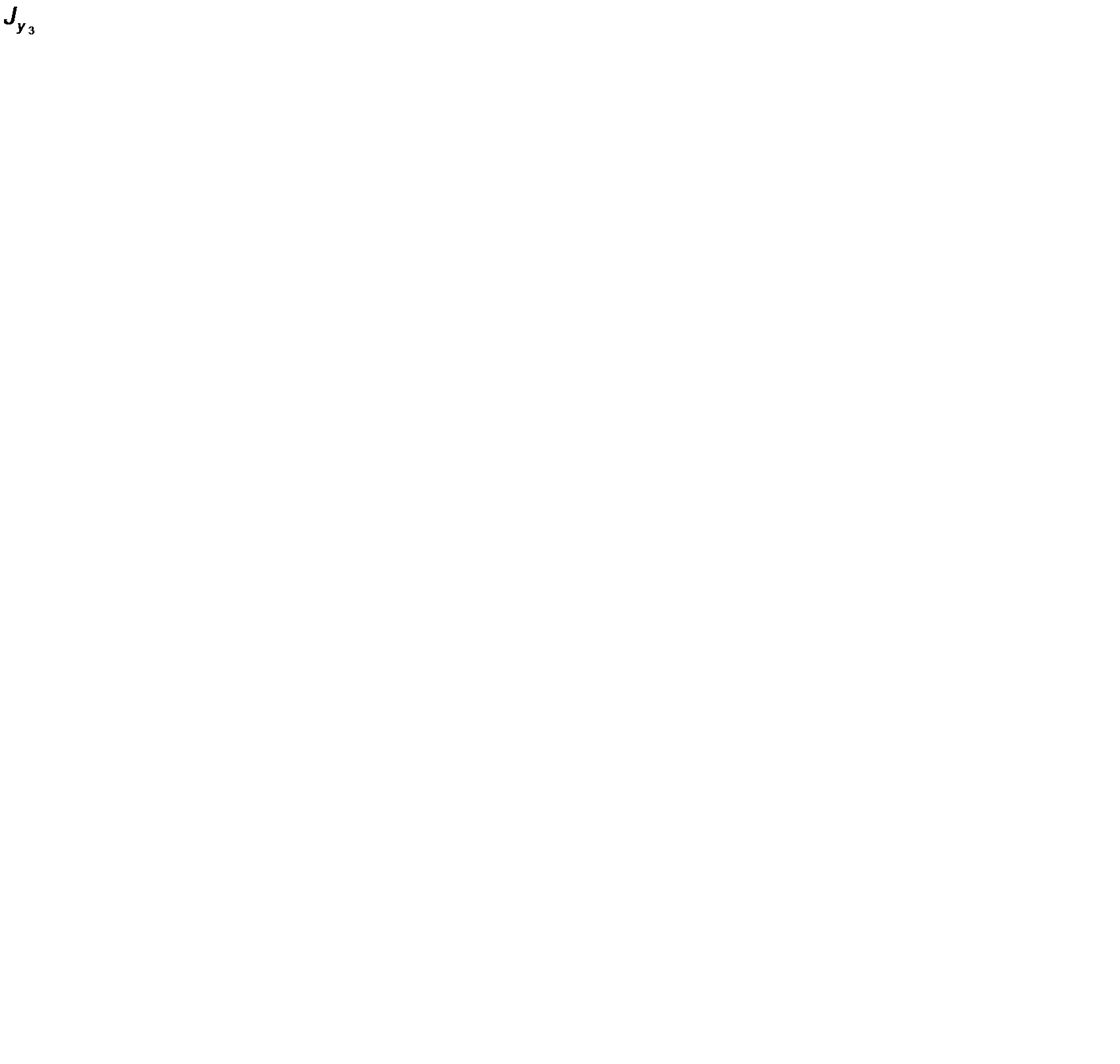 = 2900 = 2900
|  = 0 = 0
|
1). Общая площадь составного сечения
А = ∑ А i = 80+30,6+34,7 = 145,3 см2.
2). Статические моменты заданного сечения относительно осей х1 и у1
 80x16+34,7x2 – 30,6x2,7= 1270см3,
80x16+34,7x2 – 30,6x2,7= 1270см3,
 - 80x0,8+34,7x2 – 30,6x12 =380 см3.
- 80x0,8+34,7x2 – 30,6x12 =380 см3.
3). Координаты центра тяжести составного сечения
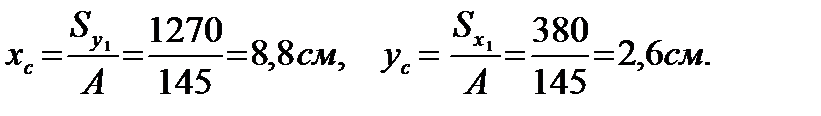
4). Координаты центров тяжести элементов сечения относительно осей х и у
точка С1: a1 =2,6+0,8= 3,4 см, b1 =16 – 8,8=7,2 см;
точка С2: а2 =5,1 – 2,6 =2,5 см, b2 =8,8+2,4 =11,2 см;
точка С3: а3 =5,1 – 2,6 = 2,5 см, b3 =8,8 – 2=6,8 см;
5). Моменты инерции сечения относительно осей х и у
 [16667 +80 ∙ 7,22] + [272 + 34,7 ∙ 6,82] +
[16667 +80 ∙ 7,22] + [272 + 34,7 ∙ 6,82] +
+ [208 + 30,6 ∙ 11,22] = 26736 см4,
 [17,06 + 80 ∙ 3,42] + [897 + 34,7 ∙ 2,52] +
[17,06 + 80 ∙ 3,42] + [897 + 34,7 ∙ 2,52] +
+ [2900 + 30,6 ∙ 9,42] = 9048 см4,
 [0 + 80 ∙ 7,2 ∙ 3,4] + [0 + 30,6 ∙11,2 ∙ 9,4] +
[0 + 80 ∙ 7,2 ∙ 3,4] + [0 + 30,6 ∙11,2 ∙ 9,4] +
+ [0 + 34,7 ∙ 6,8 ∙ 2,5] = 5502 см4.
Пример 2. Для заданного поперечного сечения стержня, состоящего из следующих фигур:
1. прямоугольника ;
2. равнобедренного треугольника 6х9 см;
3. прямоугольного отверстия 2х3 см;
необходимо определить:
- положение центра тяжести поперечного сечения (т. С);
- главные центральные оси поперечного сечения;
- главные центральные моменты инерции поперечного сечения;
- моменты сопротивления сечения.
Р е ш е н и е.
Вычисление геометрических характеристик фигур, составляющих заданное сечение, выполнено и представлено в таблице.
1). Определяем общую площадь заданного сечения
А = А1 + А2 + А3 =294 + 980 + 110,25 =1384,25 см2.
2). Определяем статический момент сечения относительно оси х1.

3). Определяем координаты центра тяжести заданного сечения.
Поскольку заданное сечение имеет ось симметрии (ось у), то центр тяжести располагается на этой оси, поэтому необходимо определить только координату ус
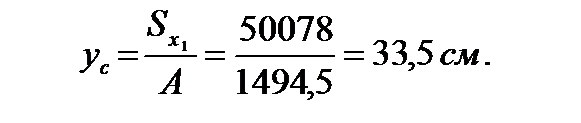
4). Через полученный центр тяжести проводим горизонтальную ось х.
Оси х, у является искомыми главными центральными осями инерции заданного сечения, т.к. ось у – ось симметрии и Jxy = 0.
5). Вычисляем главные центральные моменты инерции сечения
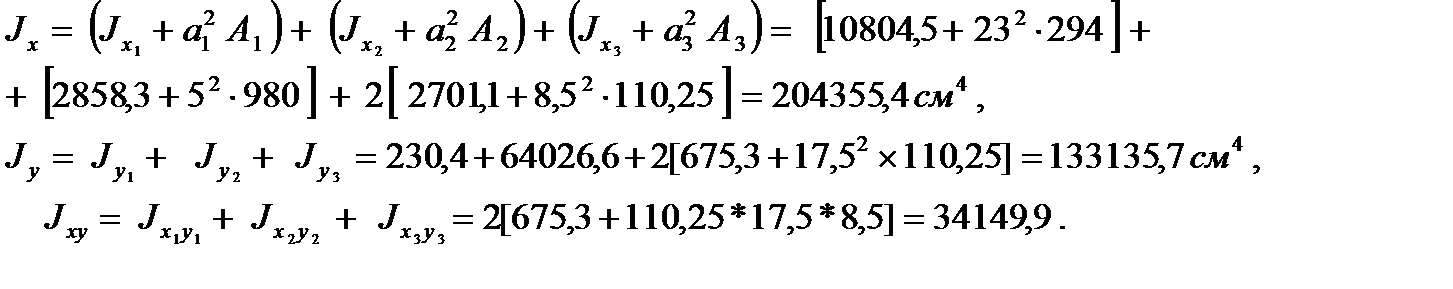
Из полученного решения следует:
Jmax = J1 = Jx = 204355,4 см4, Jmin = J2 = Jy = 34149,9 см4 .
6). Вычисляем осевые моменты сопротивления сечения
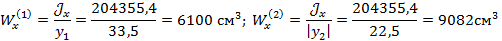
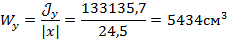
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|