Тема: Чётность, нечётность функции

Тема: Чётность, нечётность функции

Функция называется четной, если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f( ‑ x)=f(x).

Область определения четной функции симметрична относительно нуля.

График четной функции симметричен относительно оси Оу.

Функция называется нечетной, если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f( ‑ x)= ‑ f(x).

Область определения нечетной функции симметрична относительно нуля.

График нечетной функции симметричен относительно начала координат.

Если хотя бы в одной точке x∈D(f) выполняется соотношение f(−x)≠f(x) и хотя бы в одной точке x∈D(f) выполняется соотношение f(−x)≠−f(x),то функция y=f(x) не является ни чётной, ни нечётной или по-другому говоря, функцией общего вида.

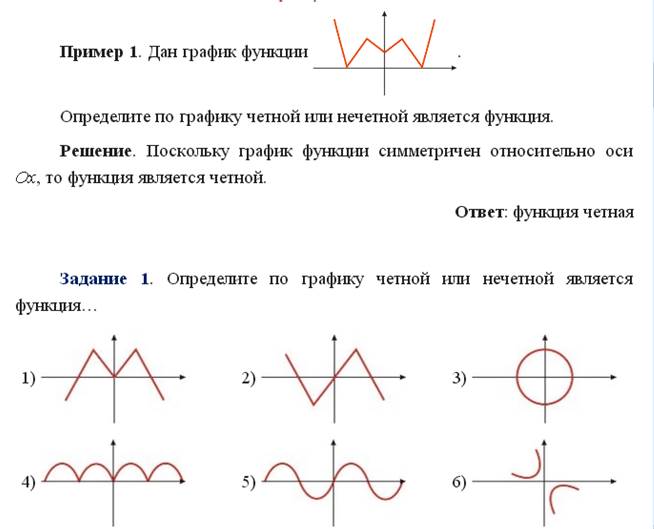
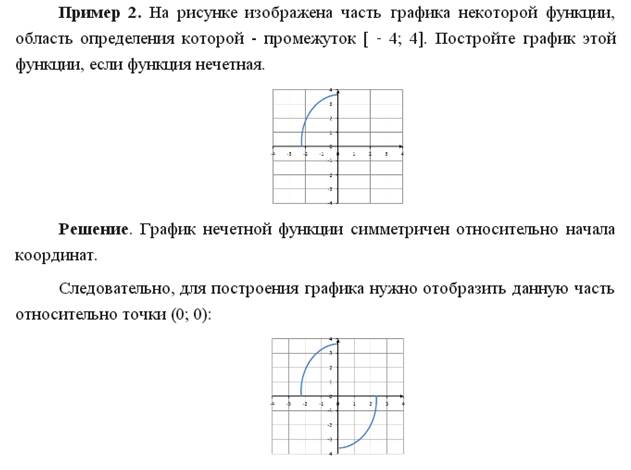
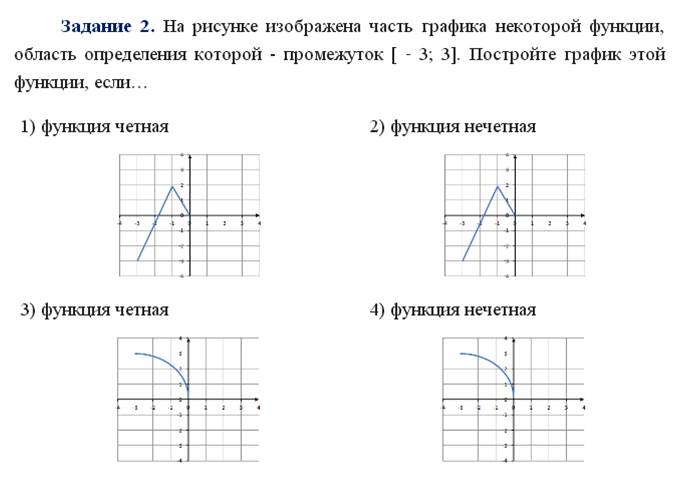
В третьем задании выполняете только то, что выделено красным кружочком, в остальных заданиях выполняете всё.