класс. Алгебра. 2 ноября. Тема: Разложение квадратного трёхчлена на множители.. Как разложить на множители квадратный трёхчлен. Теория.

9 класс. Алгебра. 2 ноября

Тема: Разложение квадратного трёхчлена на множители.

Напоминаю теоретические аспекты (у многих правильное оформление имеется в тетради по теории, смотрите прошлый год, тема: Решение квадратных уравнений).

Как разложить на множители квадратный трёхчлен

Теория.

Квадратный трёхчлен — это многочлен вида ax²+ bx + c.

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

ax²+ bx + c = 0

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

a(x − x₁)(x − x₂)

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

ax²+ bx + c = a(x − x₁)(x − x₂)

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

x²− 8x + 12

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

x²− 8x + 12 = 0

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

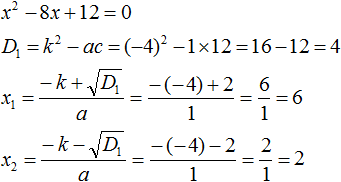
Итак, x₁= 6, x₂= 2. Теперь воспользуемся формулой ax²+ bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax²+ bx + c напишем свой квадратный трёхчлен x²− 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁= 6, x₂= 2

x²− 8x + 12 = 1(x − 6)(x − 2) = (x − 6)(x − 2)

Если a равно единице (как в данном примере), то решение можно записать покороче:

x²− 8x + 12 = (x − 6)(x − 2)

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2). Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x²− 8x + 12

(x − 6)(x − 2) = x²− 6x − 2x + 12 = x²− 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

2x²− 14x + 24

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

2x²− 14x + 24 = 0

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

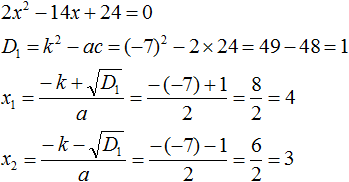
Итак, x₁= 4, x₂= 3. Приравняем квадратный трехчлен 2x²− 14x + 24 к выражению a(x − x₁)(x − x₂), где вместо переменных a, x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

2x²− 14x + 24 = 2(x − 4)(x − 3)

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x²− 14x + 24

2(x − 4)(x − 3) = 2(x²− 4x −3x + 12) = 2(x²− 7x + 12) = 2x²− 14x + 24

Задания:

№ 83