
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОНТРОЛЬНАЯ РАБОТА № 1. СОДЕРЖАНИЕ РАБОТЫ. Варианты заданий
КОНТРОЛЬНАЯ РАБОТА № 1
Перед решением задач контрольной работы необходимо по учебной литературе изучить материалы следующих тем:
- центральная и параллельная проекции;
- точка, прямая, плоскость в ортогональных проекциях;
- позиционные и метрические задачи;
СОДЕРЖАНИЕ РАБОТЫ
Контрольная работа состоит из двух заданий, выполняемых на двух листах ватмана А3.
Задание 1.1 «Метрические и позиционные задачи» включает решение следующих задач:
- определить расстояние от точки D до плоскости, заданной треугольником АВС;
- построить плоскость, параллельную плоскости, заданной треугольником АВС, и отстоящую от неё на 45 мм;
- через прямую DЕ провести плоскость, перпендикулярную треугольнику АВС, построить линию пересечения этих двух плоскостей, определить видимость геометрических элементов.
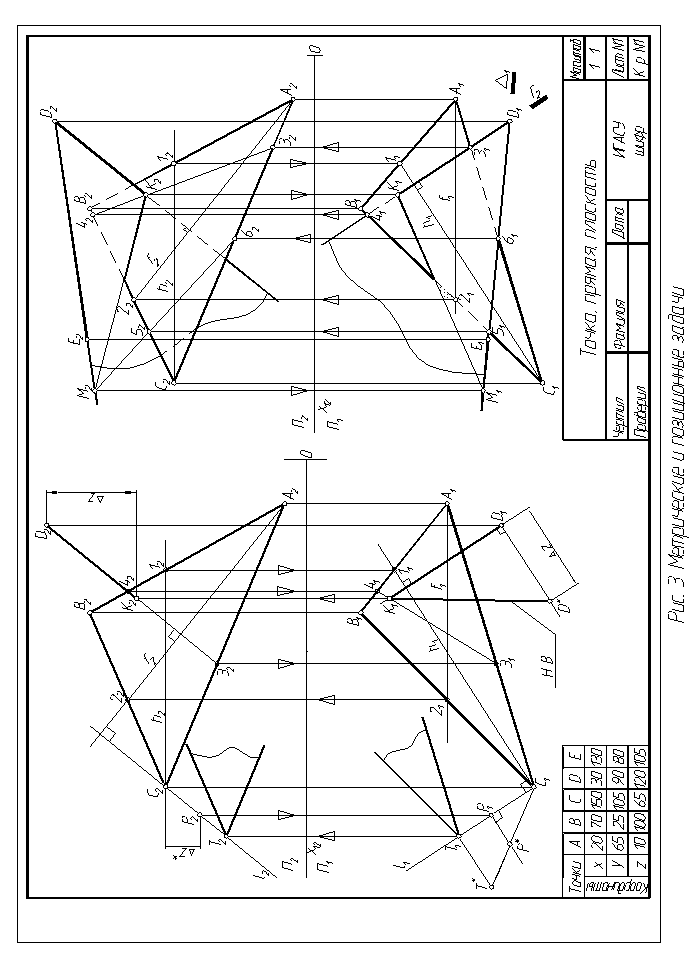
Данные для выполнения задания взять из табл. 1, в соответствии с вариантом. Координаты точек даны в миллиметрах. Работа выполняется в масштабе 1:1, на формате А3 (297×420). Пример выполнения задания 1.1 приведён на рис. 3.
Таблица 1
Варианты заданий
| Вариант | Точки | Координаты | Вариант | Точки | Координаты | ||||
| X | Y | Z | X | Y | Z | ||||
| A B C D E | A B C D E | ||||||||
| A B C D E | A B C D E | ||||||||
| A B C D E | A B C D E | ||||||||
| A B C D E | A B C D E | ||||||||
| A B C D E | A B C D E | ||||||||
Для решения данной комплексной задачи необходимо решить ряд простых задач:
1. Построить проекции точек А, В, С, D по координатам согласно своему варианту (см. табл. 1), затем объединить точки А, В, С в треугольник на каждой плоскости проекции.
2. В плоскости АВС провести фронталь f(f1, f2) и горизонталь h(h1, h2).
3. Из точки D опустить перпендикуляр к плоскости АВС. Для этого в плоскости треугольника АВС построить фронталь f(f1, f2) и горизонталь h(h1, h2). Из проекций точки D(D1, D2) согласно теореме построить перпендикуляр к плоскости.
4. Расстояние от точки D до плоскости АВС есть отрезок прямой, ограниченный с одной стороны самой точкой D, а с другой – точкой встречи К построенного перпендикуляра к h и f с плоскостью АВС. Итак, отрезок DK [(D1K1); (D2K2)] есть расстояние от точки D до плоскости АВС.
5. Для определения натуральной величины расстояния от точки D до плоскости АВС использовать метод прямоугольного треугольника. Для этого замерить разность высот точек D2 и К2; т.е. ΔZ = [D2К2], и отложить эту величину ΔZ из точки D1 перпендикулярно отрезку [D1K1] ([D1K1] ^ [D1D*], причём [D1D*] = ΔZ). Таким образом, гипотенуза [К1D*] прямоугольного треугольника К1D1D* и есть натуральная величина расстояния от точки D до плоскости АВС.
6. Через точку С или любую другую точку, принадлежащую треугольнику АВС, провести перпендикуляры к прямым h1 и f2. На этом перпендикуляре взять на произвольном расстоянии от точки С точку и найти её соответствующую проекцию.
7. Методом прямоугольного треугольника найти натуральную величину отрезка [С] на соответствующей плоскости проекции. Для этого замерить ΔZ* и отложить эту величину из точки Р1 ^ [С1Р1].
8. От точки С1 на гипотенузе прямоугольного треугольника отложить необходимую величину (ℓ =45 мм) и получить точку Т*, затем найти точки Т1 и Т2.
9. Ещё раз по заданным координатам построить проекции точек АВСDЕ и объединить точки АВС в треугольник, через точки DE провести прямую.
10. В плоскости треугольника АВС провести горизонталь h(h1, h2) и фронталь f(f1, f2).
11. Опустить, например, из точки D перпендикуляр ℓ на плоскость АВС, задать новую плоскость двумя пересекающимися прямыми: /DE/ ^ ΔABC и ℓ ^ ΔABC; /DE ∩ ℓ/.
12. Для построения линии пересечения двух плоскостей ΔABC и DE ∩ ℓ находят две точки встречи прямой /DE/ с плоскостью ΔABC (т.е. точка М) и точку встречи перпендикуляра ℓ, опущенного из точки D на плоскость АВС, с этой плоскостью (точка К).
13. Определение видимости сторон треугольников осуществляют по методу конкурирующих точек.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|