Пример 2.

Статистика. Статистическая обработка данных.

Цель лекции: формирование представлений о статистике как средстве описания явлений и процессов, связанных с массовыми статическими данными.

Задача лекции: овладение основными понятиями и методами обработки статистических данных.

Статистика – отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических (количественных или качественных) данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме.

Статистика разрабатывает специальную методологию исследования и обработки материалов: массовые статистические наблюдения, метод группировок, средних величин, метод графических изображений и другие методы анализа статистических данных.

Сначала под статистикой понимали «описание экономического и политического состояния государства или его части». И в настоящее время деятельность государственных статистических служб вполне укладываются в это описание.

Статистика состоит из трех разделов:

1. сбор статистических сведений, то есть сведений, характеризующих отдельные единицы каких – либо массовых совокупностей;

2. статистическое исследование полученных данных, заключающееся в выяснении тех закономерностей, которые могут быть установлены на основе данных массового наблюдения;

3. разработка приемов статистического наблюдения и анализа статистических данных. Последний раздел, собственно, и составляет содержание математической статистики.

Рассмотрим пример: на праздничном вечере среди учеников одиннадцатых классов провели лотерею. Каждый из пятидесяти школьников произвольно задумал одну цифру от 0 до 9 и записал её на своём лотерейном билете. Итак, имеется 50 листочков, содержащих всю необходимую информацию.

Что же делать с этой информацией? Целесообразно упорядочить и сгруппировать её. После этой перегруппировки результаты собрали в таблицу:

Ответ
Количество ответов

Всем участникам раздали небольшие призы:

- «самый популярный» (ответ 5);

- «почти самый популярный» (ответ 3);

- «оригинально, но неверно» (ответ 10);

- «сладкая парочка» (ответ 0);

- «три богатыря» (ответ 2, 6, 8);

- «отличники» (ответ 1, 7, 9);

- «хорошисты» (ответ 4)

Пока проходило награждение провели статистическую обработку данных.

Получили гистограмму распределения.По оси абсцисс отложены сами ответы (числа из первой строки таблицы), по оси ординат отложены количества ответов (числа из второй строки).

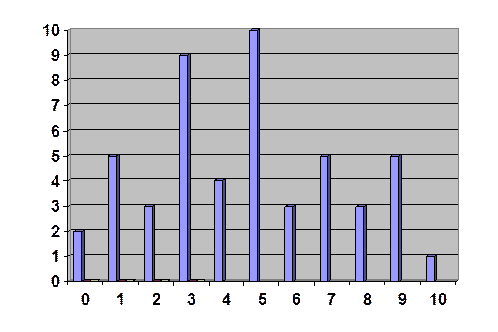
Существуют другие графические изображения распределения данных – многоугольник распределения (график зависимости количества ответов от ответов), круговая диаграмма, с которыми подробнее ознакомимся на семинарских занятиях.

Кроме того, перечислим некоторые числовые характеристики для разобранного выше измерения, а именно:

- объём измерения, в данном случае он равен 50, так как обрабатывались ответы 50 участников;

- размах измерения, в данном случае он равен 10, то есть разности между наибольшим (10) и наименьшим (0) результатами измерений (10 – 0 = 10);

- мода измерения, в данном случае она равна 5, так как ответ «5» - самый «модный», самый популярный, он встретился чаще других – 10 раз из всех 50 результатов;

- среднее (или среднее арифметическое),это частное от деления суммы всех результатов на объём измерения; в данном случае вычисления выглядят так:

(0*2 + 1*5 + 2*3 + 3*9 + 4*4 + 5*10 + 6*3 + 7*5 + 8*3 + 9*5 + 10*1)/50 = (0 + 5 + 6 + 27 + 16 + 50 + 18 + 35 + 24 + 45 + 10)/50 = 236/50 = 4,72;

- медиана измерения (средняя варианта в сгруппированном ряде данных), ряд вариант называется сгруппированным, если все варианты записаны в порядке возрастания; если средних вариант две, то медиана равна их полусумме; в рассмотренном примере получаем такой сгруппированный ряд:

0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9, 10.

В рассмотренном примере 50 вариант, средних – две, это варианты №25 и №26; обе они равны 5, значит, и медиана равна 5.

В результате обработки статистических данных возникает ещё одна характеристика ряда: абсолютная частота варианты или кратность.

Определение.Если среди всех данных конкретного измерения одна из вариант встретилась k раз, то это число называют кратностью этой варианты.

В нашем примере:

варианта

сумма

кратность

Рассмотрим несколько примеров.

Пример 1.

На уроке физкультуры 14 школьников прыгали в высоту, а учитель записывал их результаты. Получился такой ряд данных (в сантиметрах):

125, 110, 130, 125, 120, 130, 140, 125, 110, 130. 120, 125, 120, 125.

Требуется сгруппировать данные, составить таблицу их распределения, найти размах, моду и медиану измерения.

Решение. Выпишем все варианты измерения в порядке возрастания:

110, 110, 120, 120, 120, 125. 125, 125, 125, 125. 130, 130, 130, 140. это сгруппированный ряд данных.

Составим таблицу распределения:

	варианта	сумма
		сумма
кратность

Размах: 140 – 110 = 30;

Мода: 125;

Медиана: 125.

Пример 2.

В таблице распределения данных часть информации утеряна. Восстановите её, если известно, что объём измерения равен 20, размах равен 6, а мода равна 2.

	варианта		сумма
		- 1	сумма
кратность

Решение. По определению, в графе сумма должен стоять объём измерения, то есть 20. Этот объём равен сумме всех кратностей. Значит, кратность варианты «0» равна 20 – (5 + 1 + 7 + 3) = 4. Самая большая кратность равна 7. значит, над ней и расположена мода измерения, равная 2. Так как размах равен 6, а наибольшая варианта равна 3, то наименьшая варианта равна 3 – 6 = - 3. Эту варианту помещаем в последнюю свободную графу над кратностью 5. Получаем таблицу:

	варианта		сумма
	- 3	- 1	сумма
кратность

Задачи для самостоятельного решения.

1.Ученик выписал из дневника свои отметки за март. Вот что получилось: 4. 4, 3, 2, 5, 3, 3, 4, 5, 4, 4, 4, 5, 4, 2, 4, 4, 5, 3, 3.

а) составьте сгруппированный ряд этих данных;

б) чему равна мода этого измерения и какова её кратность?

в) выпишите таблицу распределения данных;

г) найдите среднее значение отметок за март

2. В очередном туре футбольного чемпионата состоялись 10 матчей. Вот их результаты:

3:1, 0:2, 1:1, 0:0, 0:4, 0:1, 2:2. 0:3, 1:0, 1:1.

Футбольный статистик подсчитал результативность матчей (количество голов).

а) выпишите (не сгруппированный) ряд полученных данных;

б) сгруппируйте его и составьте таблицу распределения данных и распределения их частей;

в) найдите среднюю результативность матчей в этом туре.

Вывод:необходимо изучить теоретический материал данной лекции и решить задания для самостоятельного решения