Школьный этап олимпиады по математике

Школьный этап олимпиады по математике

для учащихся 8 класса

2018-2019 уч.год

1. Как посадить 10 яблоней, чтобы нашлось 5 рядов, в каждом из которых ровно 4 яблони?

2. В выражении 1 – 2 – 4 - 8 – 16 = 19 расставьте несколько знаков модуля так, чтобы равенство стало верным.

3. Каждую сторону прямоугольника увеличили на 3 см, в результате чего его площадь увеличилась на 39 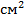. Найдите периметр исходного прямоугольника.

4. Вычислить: + + + + + + + .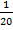

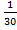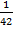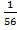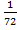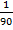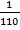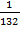5. Страницы книги пронумерованы подряд с первой до последней. Хулиган Вася вырвал из разных мест книги 25 листов и сложил номера всех пятидесяти вырванных страниц. У него получилось число 2002. Когда об этом узнал отличник Коля, то он заявил, что при счете Вася ошибся. Объясните, почему Коля прав.

Школьный этап олимпиады по математике

для учащихся 8 класса (решение)

1. (5б) Как посадить 10 яблоней, чтобы нашлось 5 рядов, в каждом из которых ровно 4 яблони?

Ответ:

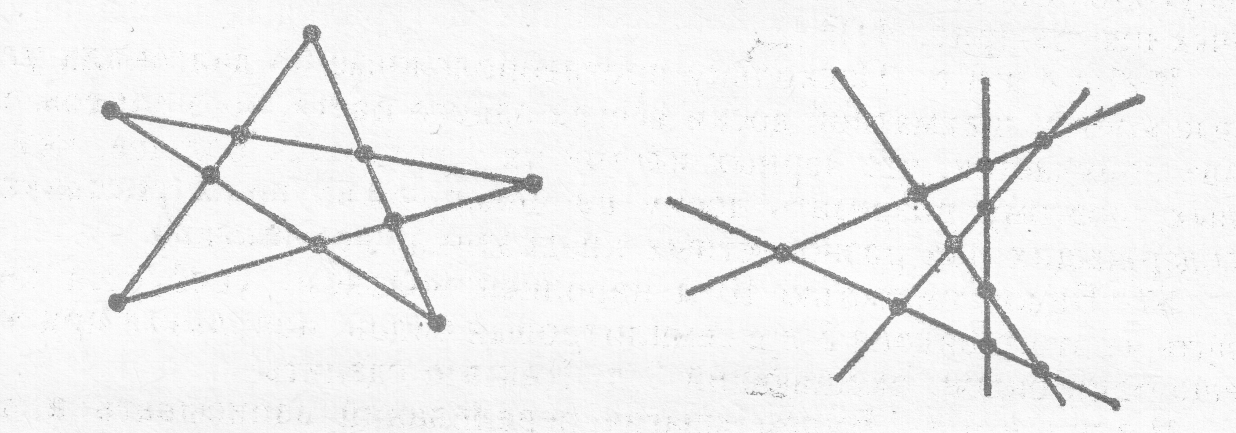
2. (5б) В выражении 1 – 2 – 4 – 8 - 16 =19 расставьте несколько знаков модуля так, чтобы равенство стало верным.

Ответ: II 1 – 2I – I 4 – 8 I – 16I = 19.

3.(5б) Каждую сторону прямоугольника увеличили на 3 см, в результате чего его площадь увеличилась на 39 Найдите периметр исходного прямоугольника.

Ответ: 20 см.

Решение:

Пусть x см – ширина прямоугольника, y см – длина прямоугольника.

(x + 3) (y + 3) – xy = 39

Xy +3x +3y +9 –xy = 39

3x + 3y = 30

X +y =10

Р = ( x + y) 2 = 10 2 = 20.

4. (5б) Вычислить + + + + + + .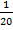

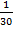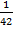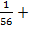
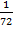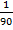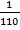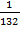Ответ: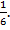

Решение:

+ + + = + + + =( ) +

( ) + ( - ) + ( - ) + (

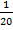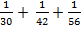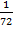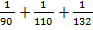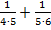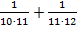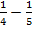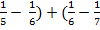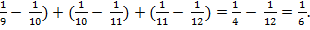
5.(5б) Страницы книги пронумерованы подряд с первой до последней. Хулиган Вася вырвал из разных мест книги 25 листов и сложил номера всех пятидесяти вырванных страниц. У него получилось число 2002. Когда об этом узнал отличник Коля, то он заявил, что при счете Вася ошибся. Объясните, почему Коля прав.

Решение:

На каждом из вырванных листов – две страницы. Номер одной из страниц – четное число, а другой – нечетное. Тогда в сумме всех номеров вырванных страниц будет 25 четных и 25 нечетных слагаемых. Поэтому сумма будет нечетной, а значит, она не может быть равна 2002.