Хелпикс

Главная

Контакты

Случайная статья



Рекуррентные алгоритмы

Стр 1 из 2Следующая ⇒


Рекуррентные алгоритмы

 

Построенные на рекуррентных формулах, математически точно описывающие соотношение между последующими и предыдущими членами последовательности. Они соответствуют методам прямого вычисления. Рекуррентные формулы компактны, легко программируются и во многом лучше точных или приближённых формул.

Так для определения полиномов Чебышева 1-го рода целого порядка имеем точную формулу:

 ;

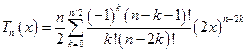а рекуррентное соотношение:

.

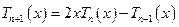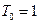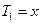; . Организуют рекурсию.

Для вычисления следующего члена составляют цикл рекурсии – совокупность операций.

Две  возможные цели рекурсий:

1. вычисление значения 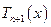 в конкретной точке ;

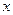2. вычисление структуры 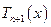, т.е. всех его коэффициентов.

 

Вычисление 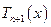 по рекурсии .

 

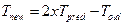Алгоритм рекурсии

 

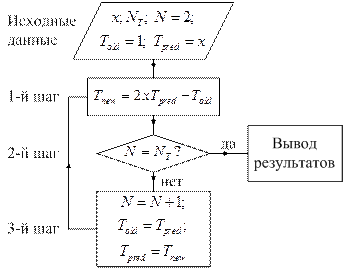
Рекурсии для расчёта коэффициентов .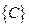

; ; .

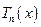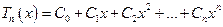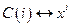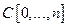Рассмотрим первые полиномы:

; ;

     ; ; ;

       ; ; ; ; .

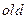
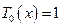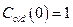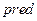
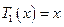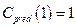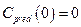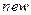
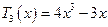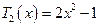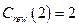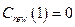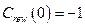Отсюда после анализа можно получить следующие рекуррентные соотношения для коэффициентов .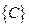

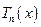Для :                    .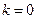

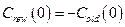Для :                              .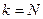

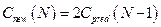Для остальных :    .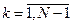

 

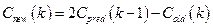Алгоритм рекурсии

 

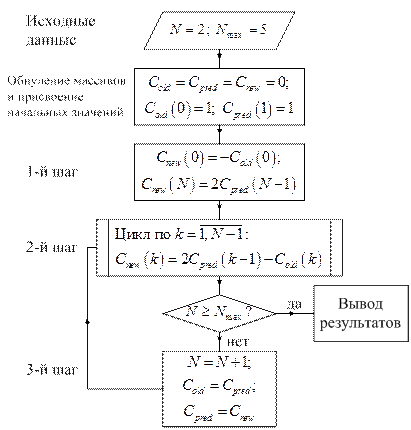
Пример использования рекурсии:

;

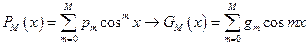Возможные пути:

1. Аналитический путь: 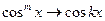 – громоздкая программа.

2. Интерполяция по сетке 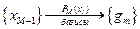 – вычислительные погрешности.

3. Формула 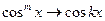 + последующая группировка подобных членов – очень громоздко, велика вероятность ошибки при написании алгоритма.

4. Рекурсии.

Используя рекурсии, можно построить преобразования на другой вычислительной основе:

;

;

;

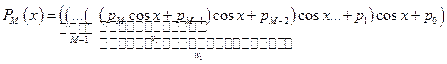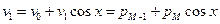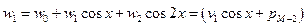Для произвольного 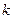 от 2 до :

;

.

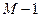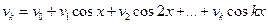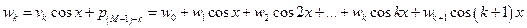При 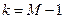 получаем .

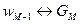Алгоритм

Для алгоритма рекурсии используем соотношение: ;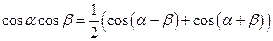

Для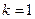

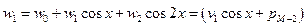 где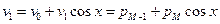

; ;

 

; ; .

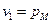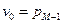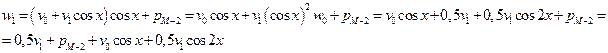
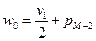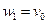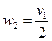Для произвольного  ( ):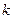

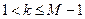Для I = 0,1; k; k+1 имеем

; ; ; .

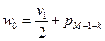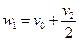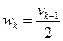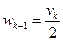Для : .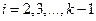

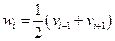Проверка: .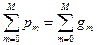

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.