ЛАБОРАТОРНАЯ РАБОТА №5. Обработка матриц. Теоретические сведения. Если в какой-то группе {…} отсутствует значение, то соответствующему элементу присваивается 0.. Свойства квадратных матриц

ЛАБОРАТОРНАЯ РАБОТА №5

Обработка матриц

Цель работы: овладение навыками алгоритмизации и программирования структур с вложенными циклами, навыками использования приемов программирования во вложенных циклах, способами ввода, вывода и обработки матриц.

5.1 Теоретические сведения

Двухмерный массив представляется как одномерный, элементы которого являются тоже массивами. Наиболее быстро изменяется последний индекс элементов массива, поскольку многомерные массивы в языке Си размещаются в памяти компьютера в последовательности столбцов.

Декларация многомерного массива:

тип ID[размер 1][размер 2]…[размер N];

Например, массив целого типа, состоящий из двух строк и трех столбцов (с инициализацией начальных значений)

int a[2][3] = {{0,1,2},{3,4,5}};

в оперативной памяти будет размещен следующим образом:

a[0][0]=0, a[0][1]=1, a[0][2]=2, a[1][0]=3, a[1][1]=4, a[1][2]=5.

Если в какой-то группе {…} отсутствует значение, то соответствующему элементу присваивается 0.

Приведем пример заполнения двумерного массива случайными числами и последующем выводом этих значений на экран.

# include <iostream>

int main () {

int n[4] [5];

for (int i=0; i<4;i++) {

for (int j=0;j<5;j++) {

n[i] [j]= rand () % 10;

cout << n[i] [j] << “ “;}

cout << “\n”;}

return 0;

}

При инизиализации многомерных массивов можно первый размер не указывать. В этом случае он определяется автоматически. Например, объявление двумерного массива может выглядеть так:

Double numbers [] [2] { { 1.1,3.2}, {8.3,5.4}, {9.5,2.6}};

Квадратная матрица- это двумерный массив, у которого количество строк и столбцов одинаково. Например массив int A[4][4] является квадратной матрицей, у которой 4 строк и 4 столбцов:

a₀₀ a₀₁ a₀₂ a₀₃

a₁₀ a₁₁ a₁₂ a₁₃

a₂₀ a₂₁ a₂₂ a₂₃

a₃₀ a₃₁ a₃₂ a₃₃

Свойства квадратных матриц

p если номер строки элемента совпадает с номером столбца (i = j), это означает что элемент лежит на главной диагонали матрицы;

p если номер строки превышает номер столбца (i > j), то элемент находится ниже главной диагонали;

p если номер столбца больше номера строки (i < j), то элемент находится выше главной диагонали.

Данные свойства главной диагонали квадратной матрицы можно представить схематически (рисунке 5.1).

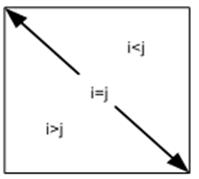
Рисунок 5.1 — Свойства главной диагонали квадратной матрицы

p элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i + j +1 = n;

p неравенство i + j + 1 < n характерно для элемента находящегося выше побочной диагонали;

p соответственно, элементу лежащему ниже побочной диагонали соответствует выражение i + j + 1 > n.

Данные свойства побочной диагонали квадратной матрицы можно представить схематически (рисунке 5.2).

Рисунок 5.2 — Свойства побочной диагонали квадратной матрицы

При работе с многомерными массивами следует иметь виду, что такие структуры занимают достаточно много места в памяти. Если, например, на запись одного элемента массива отводится 4 байта, то одномерный массив из 100 элементов занимает 400 байт, а двумерный массив – 40000 байт. С увеличением размерности массива размер увеличивается в геометрической програссии, поэтому на практике массивы размерности большей второй используются редко.

12 3 Следующая ⇒