
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. ВТОРОГО ПОРЯДКА. С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.. Пример.. Пример.. Пример.. УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВТОРОГО ПОРЯДКА
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.
Линейное дифференциальное уравнения второго порядка с постоянными коэффициентами имеет вид:
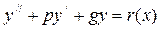
где p, g – некоторые действительные числа, r(x) – некоторая функция. Мы будем рассматривать однородные уравнения (r(x) = 0), т.е. уравнения вида
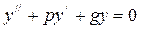
Рассмотрим решение линейного однородного уравнения с постоянными коэффициентами.
Для нахождения общего решения однородного уравнения составляем его характеристическое уравнение:
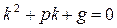 .
.
Находим его корни. При этом, если:
1. корни вещественные различные, т.е. 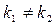 , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
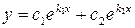
2. корни вещественные кратные, т.е. 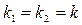 , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
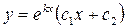
3. корни комплексные, т.е. 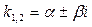 , то общее решение имеет вид:
, то общее решение имеет вид:
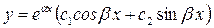
Пример.
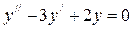 .
.
Решение.
Запишем и решим характеристическое уравнение:
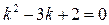 ,
,
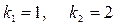 .
.
Тогда общее решение данного уравнения имеет вид:
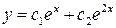 .
.
Пример.
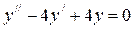 .
.
Решение.
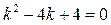 ,
,
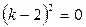 ,
,
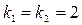 - корни кратные, вещественные,
- корни кратные, вещественные,
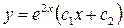 - общее решение.
- общее решение.
Пример.
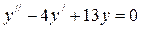 .
.
Решение.
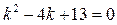 ,
,
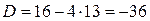 ,
,
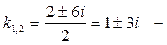 корни комплексные,
корни комплексные,
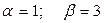
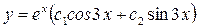 - общее решение.
- общее решение.
УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.Доказать, что для данных дифференциальных уравнений указанные функции являются решениями при любом значении 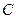 , найти частные решения, удовлетворяющие заданным начальным условиям:
, найти частные решения, удовлетворяющие заданным начальным условиям:
1. 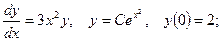
2. 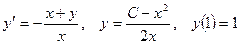 .
.
2.Найти общие решения уравнений с разделяющимися переменными:
1. 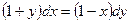 ;
;
2. 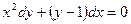 .
.
3.Решить однородные дифференциальные уравнения первого порядка:
1. 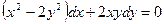 ;
;
2. 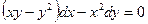 .
.
4.Решить линейные дифференциальные уравнения первого порядка:
1. 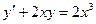 ;
;
2. 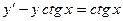 .
.
5.Решить дифференциальные уравнения:
1) 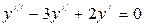 ; 4)
; 4) 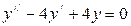 ;
;
2) 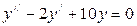 ; 5)
; 5) 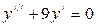 ;
;
3) 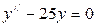 ; 6)
; 6) 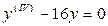 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|