Комплексный чертеж геометрических объектов.

Комплексный чертеж геометрических объектов.

В основе получения изображения предмета на плоскости лежит метод ортогонального проецирования. Сущность метода заключается в том, что предмет проецируется на взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим плоскостям (рис. 1а).

Ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость.

Плоскость П₁ называется горизонтальной плоскостью проекций, П₂ – фронтальной плоскостью проекций, П₃ – профильной плоскостью проекций. Все плоскости взаимно перпендикулярны и пересекаются друг с другом по осям: П₁ и П₂ пересекаются по оси х, П₁ и П₃ по оси у, П₂ и П₃ по оси z. Плоскости П₁, П₂ и П₃ бесконечны и непрозрачны.

Для получения плоского чертежа, с плоскостью П₂ совмещают плоскость П₁ вращением ее вокруг оси х и плоскость П₃ вращением ее вокруг оси z (рис. 1б).

Каждая из ортогональных проекций точки А определяется двумя координатами: горизонтальная проекция А₁ определяется координатами x и y, фронтальная проекция А₂ – координатами x и z, профильная проекция А₃ – координатами y и z. Каждая из проекций определяется на пересечении соответствующих координат (рис. 1б).

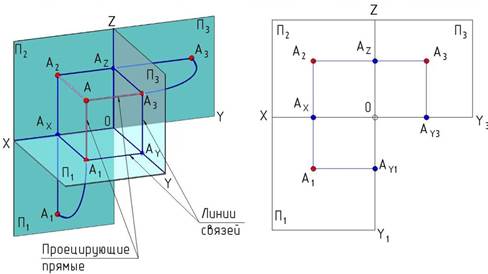
а) б)

Рисунок 1 – Ортогональная система трех плоскостей проекций: а) в пространстве; б) плоский чертёж

Прямые линии, соединяющие разноименные точки на эпюре, называются линиями проекционной связи.

Эпюр – чертёж, на котором пространственная фигура изображена методом проецирования на плоскости проекций.

Задача. Построить проекции фигуры по координатам точек: А (5,1,1), В (1,1,1), С (3,4,1), D (3,3,6).

Решение задачи показано на рис. 4.

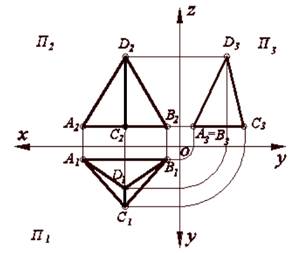
Рисунок 4 – Построение проекции пирамиды по координатам точек