Хелпикс

Главная

Контакты

Случайная статья



Вариант 5. Вариант 6. Построение графиков

⇐ ПредыдущаяСтр 3 из 3


Вариант 5

1. Вычислить производную: а) у=cos5x; б) у=73х-1

2. Вычислить производную в точке х0=0: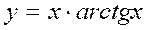

3. Найти промежутки монотонности и экстремумы функции:  а) ;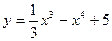

4. Найти промежутки вогнутости, выпуклости, точки перегиба: ;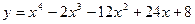

5. Исследовать на монотонность и выпуклость и построить график: .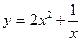

Вариант 6

1. Вычислить производную: а) у= 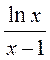 б)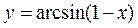

2. Вычислить производную в точке  x0=0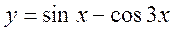

3. Найти промежутки монотонности и экстремумы функции: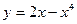

4. Найти промежутки вогнутости, выпуклости, точки перегиба: .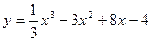

5. Исследовать на монотонность и выпуклость и построить график: .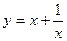

ПРИМЕР.

Исследовать на монотонность и выпуклость построить график функции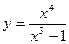     

Решение:

Воспользуемся планом полного исследования функции.

1. Область определения.

Функция определена на всей числовой оси кроме точки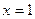

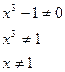
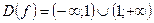
2. Точек пересечения с осями координат.

А) с осью ох А (0,0):  у=0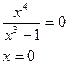

Б) с осью оу А (0,0): х=0 у(0)=0

Итак, единственная точка пересечения с осями координат (0; 0)

3. Промежутки возрастания и убывания функции, точки экстремума.

Находим производную первого порядка:

Применяемые формулы: ’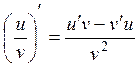 

1.

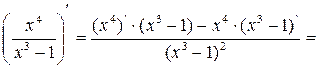
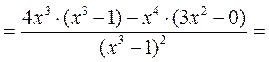
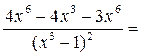
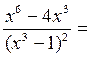
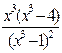
2.

  

   , ,

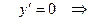
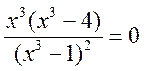
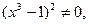
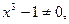
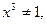
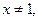
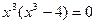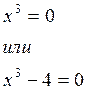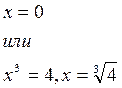
3. Производная 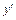 обращается в нуль при  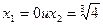и не существует при 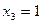. Однако, критическими точками являются только точк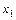и  и 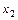: они лежат внутри области определения функции  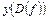и в них эта функция непрерывна. Точка .

 

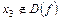4. Исследуем критические точки по знаку производной .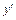

 
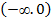
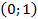
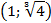
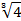
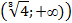
у Не сущ.
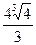
y` + - Не сущ.   - +
    max       min    

Найдём значение производной в каждом из интервалов:

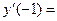
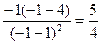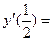
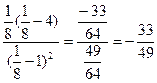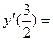
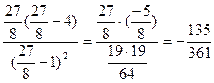> 0                                < 0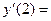

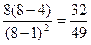< 0      > 0

 

Если на некотором промежутке 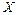 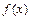имеет производную  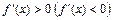для 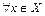, то на  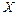функция возрастает  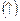(убывает ).

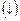Следовательно, функция возрастает 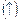 на ,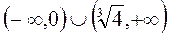

убывает 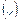 на .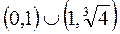

4. Если 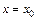– критическая точка  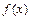и производная  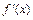при переходе через точку  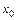меняет знак, то функция имеет в данной точке экстремум:

       максимум, если знак производной меняется с «+» на «–»,

       минимум, если знак производной меняется с «–» на «+».

Найдём значения функции в критических точках:

                                                 

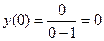
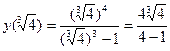
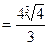
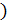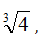
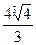
т. (0  0 -точка максимума, т. ( 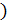-точка минимума

5. Направления выпуклости и точки перегиба.

Находим производную второго порядка

 

 

 

       

,   

                               

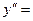
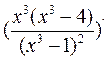
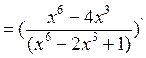
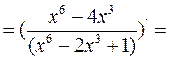
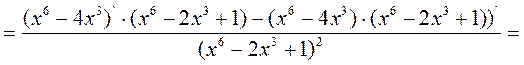
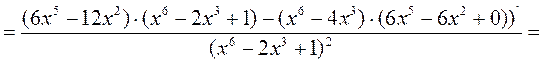
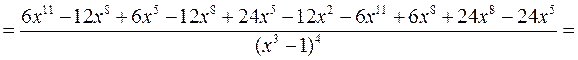
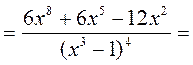
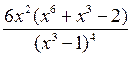
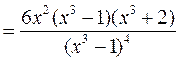
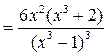
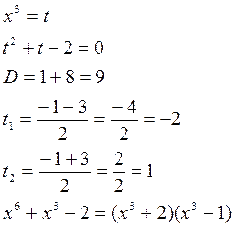
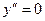
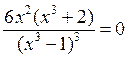
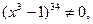
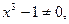
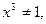
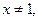
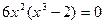
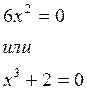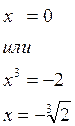
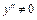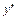    Имеем  и  не существует при 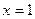, но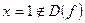

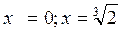точеки перегиба

 

1. Находим интервалы выпуклости функции 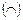 и вогнутости :

 
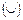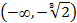
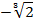
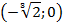
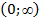
у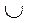  
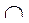
y`` + -     +

 

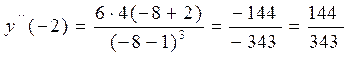
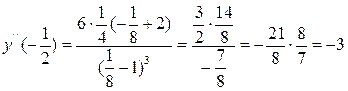
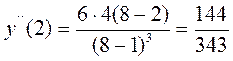
Если во всех точках 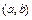: 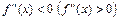, то кривая  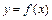на этом интервале выпукла (вогнута).

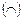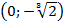Т.е. функция выпукла на и

вогнут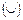а  на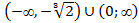

 

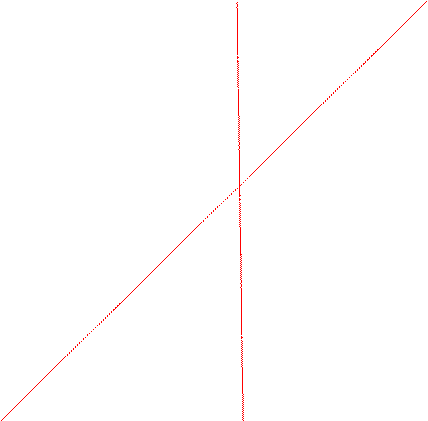
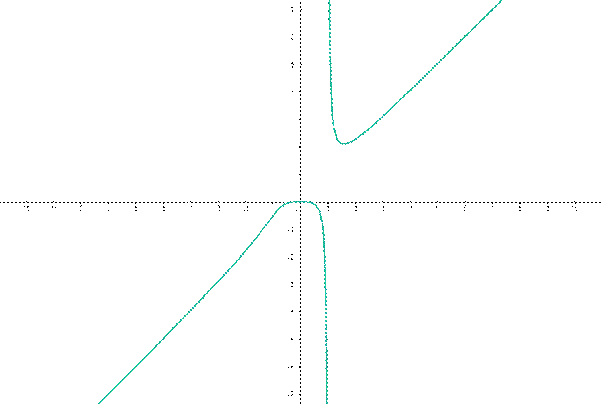
Построим график функции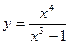

 

 

 


y=
x = 1
y = x

 


Построение графиков

https://math.semestr.ru/math/plot.php

 


⇐ Предыдущая123
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.