
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа № 1.. Задание № 1.. Задание № 2.. Задание № 3.. Задание № 4.. Задание № 5.
Контрольная работа № 1.
Тема: множества и операции над ними.
Задание № 1.
Даны множества:
А – множество четных однозначных чисел,
B – множество нечетных однозначных чисел,
С – множество чисел, кратных 3.
Установите, в каком отношении находятся множества А, В, С и изобразите их при помощи кругов Эйлера.
Задание № 2.
Задайте множество с помощью перечисленных элементов:
а) X={x/x 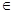 N, 0
N, 0 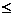 x
x 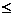 4};
4};
б)X={x/x 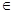 N, -2
N, -2 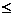 x
x 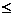 6};
6};
в)X={x/x 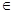 Z, -3
Z, -3 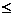 x
x 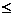 5};
5};
г)X={x/x 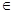 Z, 0
Z, 0 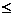 x
x 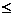 4};
4};
Задание № 3.
В данном множестве все элементы, кроме одного, обладают некоторым свойством. Опишите это свойство и найдите элемент, не обладающий им:
а) {треугольник, квадрат, трапеция, круг, правильный шестиугольник};
б) { лев, лисица, гиена, слон, рысь };
в) {бежать, смотреть, синий, знать, читать};
г) {2, 6, 15, 84, 156};
д) {1, 9, 67, 81, 121}.
Задание № 4.
Изобразите на кругах Эйлера-Венна в каких отношениях находятся множества A,B,C,D,E.
А – множество цифр в записи числа {1, 2, 3, 4, 5, 6}
Б – множество цифр в записи числа {1, 2, 12, 21}
C – множество цифр в записи числа {7, 12, 45}
D – множество цифр в записи числа {4, 5, 7, 9}
E = {12}
Задание № 5.
Известно, что D – множество деревьев в саду, F – множество фруктовых деревьев в этом саду, K – множество яблонь в этом саду. Установите, каковы отношения между парами этих множеств, если все они непустые. Изобразите множества D, F, K при помощи кругов Эйлера.
Задание № 6.
Из 170 спортсменов 70 занимаются футболом, 95 – хоккеем и 80 – теннисом. 30 занимаются и футболом, и хоккеем, 35 – и футболом, и теннисом, 15 – и хоккеем, и теннисом. 5 занимаются всеми 3 видами спорта. Сколько занимаются ровно 1 видом спорта?
Задание № 7.
Из 170 спортсменов 70 занимаются футболом, 95 – хоккеем и 80 – теннисом. 30 занимаются и футболом, и хоккеем, 35 – и футболом, и теннисом, 15 – и хоккеем, и теннисом. 5 занимаются всеми 3 видами спорта. Сколько занимаются ровно 2 видами спорта?
Задание № 8.
Запишите, используя символы:
а) число 14 — натуральное;
б) число -7 не является натуральным;
в) число 0 — целое;
г) 7 — число действительное.
Задание № 9.
Даны два множества: X = {2, 4, 6} и Y = {0, 2, 4, 6, 8}.
Верно ли что:
а) множества X и Y пересекаются;
б) множество X является подмножеством множества Y;
в) множество P = {4, 0, 6, 8, 2} равно множеству Y?
Задание № 10.
Укажите множества, о которых идет речь в следующих задачах, и какую операцию над множествами надо выполнить, прежде чем ответить на вопрос задачи:
а) У школы посадили 3 липы и 4 рябины. Сколько всего деревьев посадили у школы?
б) Детям купили 5 мячей: 3 красных, а остальные синие. Сколько синих мячей купили?
Задание № 11.
Пусть даны множества A={1,3,7,137} B={3,7,23} C={0,1,3,23} D={0,7,23,2004} Найдите множества:
1) A∪B;
2) A∩B;
3) A∪B∪C
4) D∪B∪C
5) D∪C
6) A∩B∩C;
Задание № 12.
Верно ли, что для любых множеств A, B, C
1) A∩∅=∅
2) A∪∅=A;
3) A∪A=A
4) A∩A=A
3) A∩B=A⇔A⊂B
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|