Теоретическая часть. Правила перевода ЗЛП к каноническому виду. Пример

Стр 1 из 2Следующая ⇒

Теоретическая часть

Существуют 4 основных признака представления задачи линейного программирования в канонической форме:

1) минимизация целевой функции;

2) запись системы ограничений в виде строгих равенств;

3) условие неотрицательности на все переменные;

4) наличие в системе ограничений исходного опорного решения.

Правила перевода ЗЛП к каноническому виду

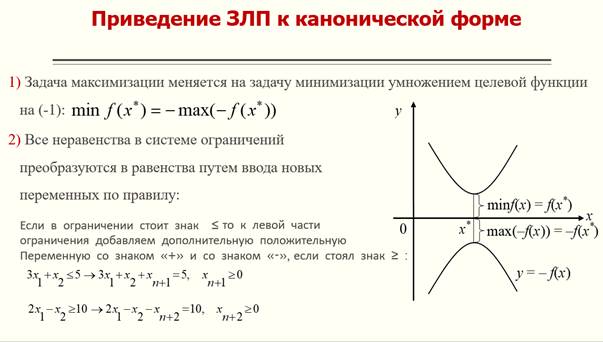
Пример

Привести к канонической форме следующую задачу линейного программирования:

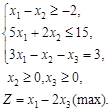
Решение:

1. Минимизируем целевую функцию задачи путем введения новой функции Z₁:
Z₁ = –Z = –x₁ + 2x₃(min).

2. В системе ограничений ЗЛП перейдем к строгим равенствам, для чего введем неотрицательные балансовые переменные x₄и x₅ в левые части неравенств со знаками минус и плюс (в зависимости от знака неравенства). В результате ЗЛП записывается в следующем виде:

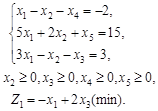
3. Перейдем к преобразованию условий неотрицательности. Данное условие не наложено только на одну переменную x₁ (назовем ее произвольной). Исключим эту переменную из задачи, выполнив следующую замену переменных:

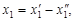где .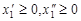

При этом получаем следующее:

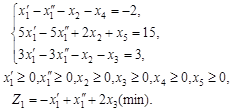
4. Выделяем в системе ограничений базис при неотрицательных свободных членах используя метод поиска исходного опорного решения.

12 Следующая ⇒