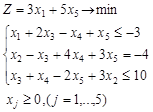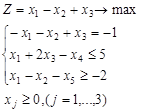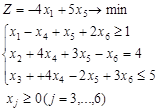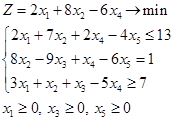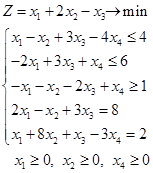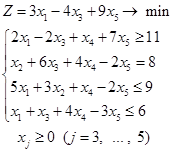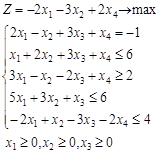- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теоретическая часть
Теоретическая часть
Каждой ЗЛП можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей ЗЛП, состоящей в нахождении максимального значения функции
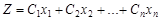 (1)
(1)
при условиях:
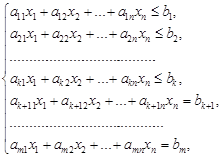 (2)
(2)
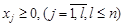 . (3)
. (3)
Определение. Задача, состоящая в нахождении минимального значения функции
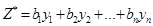 (4)
(4)
при условиях:
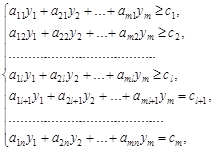 (5)
(5)
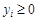 , (6)
, (6)
называется двойственной по отношению к задаче (1) — (3).
Задачи (1) — (3) и (4) — (6) образуют пару задач, называемую двойственной парой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
1. Целевая функция исходной задачи (1) — (3) задается на максимум, а целевая функция двойственной (4) — (6) — на минимум.
2. Mатрица:
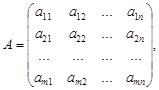
составленная из коэффициентов при неизвестных в системе ограничений (2) исходной задачи, и аналогичная матрица

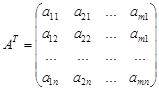
в двойственной задаче получаются друг из друга транспонированием.
3. Число переменных в двойственной задаче равно числу соотношений в системе (4) исходной задачи, а число ограничений в системе (5) двойственной задачи — числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (4) двойственной задачи являются свободные члены в системе (2) исходной задачи, а правыми частями в соотношениях системы (5) двойственной задачи — коэффициенты при неизвестных в целевой функции (1) исходной задачи.
5. Если переменная 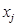 исходной задачи может принимать только лишь положительные значения, то j-е условие в системе (5) двойственной задачи является неравенством вида ³. Если же переменная
исходной задачи может принимать только лишь положительные значения, то j-е условие в системе (5) двойственной задачи является неравенством вида ³. Если же переменная 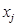 может принимать как положительные, так и отрицательные значения, то j-е соотношение в системе (5) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2) исходной задачи и переменными двойственной задачи. Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-я переменная двойственной задачи
может принимать как положительные, так и отрицательные значения, то j-е соотношение в системе (5) представляет собой уравнение. Аналогичные связи имеют место между ограничениями (2) исходной задачи и переменными двойственной задачи. Если i-е соотношение в системе (2) исходной задачи является неравенством, то i-я переменная двойственной задачи 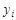 ³ 0. В противоположном случае переменная
³ 0. В противоположном случае переменная 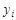 может принимать как положительные, так и отрицательные значения.
может принимать как положительные, так и отрицательные значения.
Практическое задание
Cоставить (в тетради) двойственную задачу для заданной:
Вариант 1.
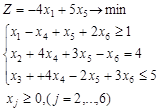
| Вариант 2.
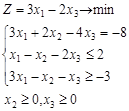
| ||
Вариант 3.
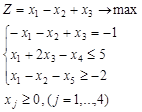
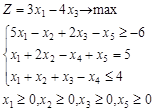
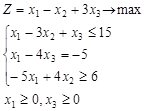
Вариант 6.
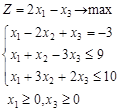
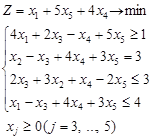
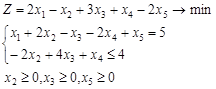
Вариант 9.