Хелпикс

Главная

Контакты

Случайная статья



Урок 3. Основное уравнение динамики



Урок 3. Основное уравнение динамики

Д.З. :2.13, 2.14, 2.21,2.22, 2.23, 2.29, 2.30, 2.31, 2.32, 2.34

По ссылке находится видео- урок3 с подробными решениями и рисунками задач: https://cloud.mail.ru/public/5F4e/eCJPV4JLa

Теория по динамике.

Действие одного тела на другое характеризуется силой. На тело действует столько сил, со сколькими телами оно взаимодействует. Инерция – это свойство тела сохранять свое состояние покоя или движения. Мерой инертности тела является его масса.

I закон Ньютона. Тело покоится или движется равномерно и прямолинейно, пока на него не действуют другие тела, или их действие скомпенсировано. Системы отсчета, в которых выполняется I закон Ньютона (закон инерции), называются инерциальными.

II закон Ньютона. Ускорение, с которым движется тело, прямо пропорционально действующей силе, обратно пропорционально массе и направлено в сторону действующей силы

                                                  .

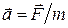III закон Ньютона. Силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению

                                                 .

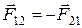Силы. В основе всех механических явлений лежит два вида взаимодействия: гравитационное и электромагнитное. Гравитационное взаимодействие двух неподвижных материальных точек описывается законом всемирного тяготения

                                                ,

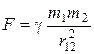гдеg = 6,67×10-11 м3/(кг×с2)- гравитационная постоянная; m1 и m2 - массы материальных точек; r12 - расстояние между точками; направлена сила по прямой, соединяющей точки.

На практике широко применяют следующие силы:

сила тяжести (обусловлена притяжением Земли и направлена вертикально вниз)

                                                  ,

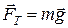сила упругости (контактная сила, направлена противоположно деформации)

                                                ,

сила трения скольжения (контактная сила, направлена противоположно скорости)

                                                 ,

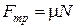сила вязкого трения (при движении тела в жидкости или газе) зависит от скорости тела и направлена против скорости; при малых скоростях она пропорциональна скорости, а при больших - квадрату скорости:

                                       , .

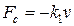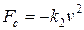Здесь g - ускорение свободного падения, k - коэффициент упругости; 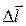 - деформация тела, m - коэффициент трения; N - сила нормального давления, прижимающая трущиеся поверхност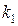и,  и  - коэффициенты сопротивления.

Задача1. Вертолёт, массой 30 тонн, поднимает на тросах вертикально вверх груз, массой 10 тонн с ускорением 1 м/. Найдите силу тяги вертолета и силу, действующую со стороны груза на прицепной механизм вертолета.

Решение: Сделав рисунок и расставив силы, получим уравнения 2 закона Ньютона для вертолета и груза в проекциях на ось У, направленную вертикально вверх:

для груза: T - mg = ma, T = m(g+a) = 110 кН

для вертолета: F - Mg - T = Ma, F = (M+m)(g+a) = 440 кН

Задача 2. На концах нити, перекинутой через неподвижный блок, подвешены тела массой m=240 г. каждое. Какую массу M должен иметь добавочный груз, положенный на одно из тел, чтобы каждое из них прошло за 4 с. 160 см.

Решение:

 Ось ОХ направим вертикально вниз и запишем 2-ой з-н Ньютона для проекций сил на ОХ: (m + Δm)•a = (m + Δm)•g - T (1) -m•a = m•g - T (2)

 Вычтем из 1-го уравнения 2-е: (m + Δm)•a + m•a = Δm•g 2•m•a + Δm•a = Δm•g 2•m•a = (g - a)•Δm

Определим а из формулы: S = a•t^2 / 2 a = 2•S / t^2

Вычислим а: а = 2•1,6 / 16 = 0,2 м/с^2

откуда: Δm = 2•m•a / (g - a)

Вычислим Δm: Δm = 2•0,24•0,2 / (9,8 - 0,2) = 0,096 / 9,6 = 0.01 кг

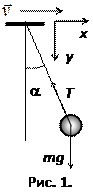Задача 3. К потолку трамвайного вагона подвешен на нити шар. Вагон тормозит и его скорость равномерно изменяется за время Δt = 3 с от v1 = 18 км/ч до
v2 = 6 км/ч. На какой угол α отклонится при этом нить с шаром?

Решение.На рис. 1.6 изображено положение шара при торможении вагона. На шар действует сила тяжести mg и натяжения нити Т.Запишем II-й закон Ньютона для шара

   .

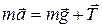Спроектируем это уравнение на оси х и у, указанные на рис. 1.

   ,

   ,

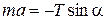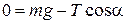где a - угол отклонения нити от вертикали.

Отсюда получим

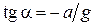   .   (1)

Ускорение шара равно ускорению вагона, которое найдем по формуле

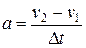   . (2)

Подставляя (2) в (1) и учитывая, что 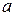< 0, получим

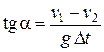 = 0,113, a = 6°30¢.

 

Задача 4. Невесомый блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы α = 30° и β = 45° (рис. 2). Грузы А и В равной массы 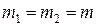 = 1 кг соединены нитью, которая перекинута через блок. Найти ускорение а, с которым движутся гири, и натяжение нити Т. Трением грузов А и В по наклонной плоскости, массой и растяжением нити, а так же трением в блоке и массой блока пренебречь.

Решение. Т.к. грузы соединены нерастяжимой нитью, то они будут двигаться с одинаковыми по величине, но разными по направлению, скоростью и ускорением. Кроме того, натяжение нити по разные стороны блока будет одинаковым, т.к. нить и блок невесомые и трение в блоке отсутствует. Движение каждого груза лучше рассматривать в локальной системе координат для каждого груза, одна ось которой направлена вдоль наклонной плоскости, а другая – перпендикулярно (рис. 2). Из рис. 1.7 следует, что 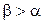, поэтому груз А будет опускаться, а В – подниматься. Тогда по II закону Ньютона в проекциях на оси х для каждого груза имеем

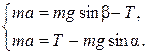      (1)

Сложив почленно эти уравнения, получим

   ,

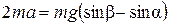откуда найдем ускорение

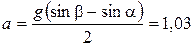 м/с2.

Из второго уравнения (1), подставив ускорение а, найдем натяжение нити

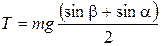= 5,9 Н.

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.