- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Треугольник
Стр 1 из 2Следующая ⇒
Треугольник
| Обозначения: А, В, С — вершины, а также углы при этих вершинах; а, b, с — стороны, противолежащие углам А, В, С соответственно; ha , hb , hc — высоты, опущенные на стороны а, b, с соответственно; ma , mb , mc — медианы; la , lb , lc — биссектрисы; R — радиус описанной окружности; r — радиус вписанной окружности. | 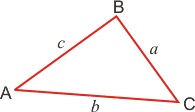
| ||||||||
|
| |||||||||
Подобие треугольников
|
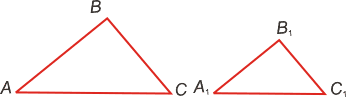
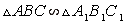 Если треугольники подобны, то Если треугольники подобны, то 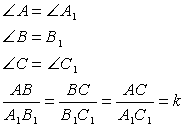
| ||||||||
|
| |||||||||
Пропорциональные отрезки в треугольнике
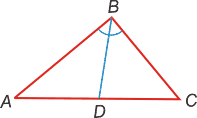
Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:
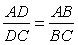
| 
| ||||||||
|
| |||||||||
| Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение. Высоты треугольника пересекаются в одной точке О,называемой ортоцентром. Втупоугольном треугольнике ортоцентр лежит вне треугольника. Впрямоугольном он совпадает с вершиной прямого угла. | 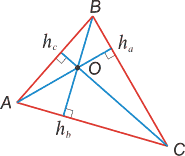 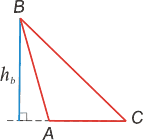
| ||||||||
|
| |||||||||
| Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника. Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины). | 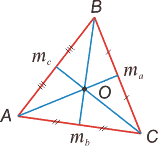
| ||||||||
|
| |||||||||
| Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Биссектрисой угла называется луч, делящий угол пополам. Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности. | 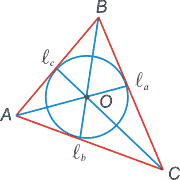
| ||||||||
|
| |||||||||
Равенство треугольников
| 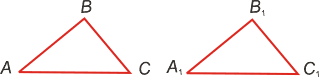 Два треугольника называются равными, если при наложении друг на друга они совместятся.
Два треугольника называются равными, если при наложении друг на друга они совместятся.
и соответственные углы равны
| ||||||||
|
| |||||||||
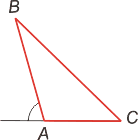
| Неавенства треугольника Всякая сторона треугольника меньше суммыи больше разности двух сторон Внешний угол треугольника больше любого внутреннего угла, не смежного с ним. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. | 
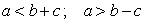
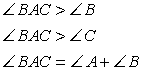
| ||||||||
|
| |||||||||
| Площадь треугольника | 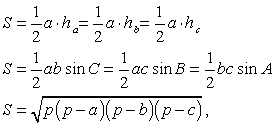 где р — полупериметр треугольника (формула Герона). где р — полупериметр треугольника (формула Герона).
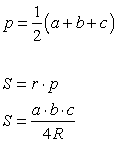
| ||||||||
|
| |||||||||
| Медиана, биссектриса, высота | 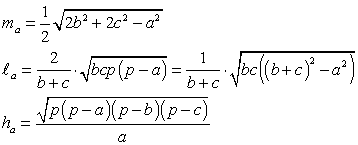
| ||||||||
|
| |||||||||
| Высоты и стороны треугольника | 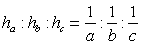
| ||||||||
|
| |||||||||
| Теорема косинусов | 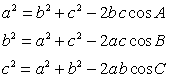
| ||||||||
|
| |||||||||
| Теорема синусов | 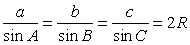
| ||||||||
|
| |||||||||
| Теорема тангенсов | 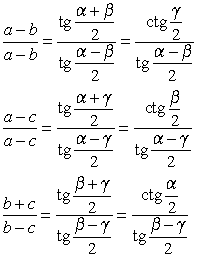
| ||||||||
|
| |||||||||
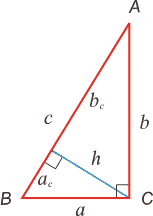
Прямоугольный треугольник
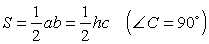 Теорема Пифагора
Теорема Пифагора
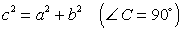
| 
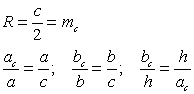
| ||||||||
|
| |||||||||
Равносторонний треугольник
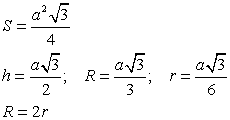
| 
| ||||||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|

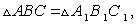 то соответственные стороны равны
то соответственные стороны равны