Тема 2. Механические передачи. Лекция 7. Передача планетарная.

Тема 2. Механические передачи. Лекция 7. Передача планетарная.

Планетарные передача – это передача с колесами, оси которых подвижны и перемещаются вокруг окружностей других колес, будучи с ними связанными, т.е. представляют собой эпициклическую передачу, в которой на отдельные звенья наложена кинематическая связь (Рисунок 2.31).

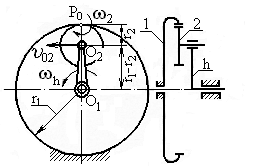
Рисунок 2.31 – Схема трехзвенного планетарного механизма:

1 – колесо центральное; 2 – сателлит; h– водило

Звено h входит во вращательные пары О₁ со стойкой и О₂ с зубчатым колесом 2 и вращается с угловой скоростью w_h. Звено 2 обегает центральное неподвижное колесо 1, вращаясь с угловой скоростью w₂ вокруг мгновенного центра вращения Р₀. Звено 1 называют центральным колесом, звено 2 – сателлитом, звено h –водилом.

Механизмы, в которых хотя бы одно звено имеет подвижную ось называют сателлитными. Сателлитные механизмы с одной степенью подвижности являются планетарными. Передаточное отношение в таких передачах устанавливается по связи угловых скоростей w₂ и w_h через линейную скорость v_O₂ точки O₂,общей для колеса 2(сателлита) и водила h

v_O₂=w₂×r₂= – w_h×(r₁ – r₂), (2.133)

где r₁ и r₂ – радиусы центрального колеса и сателлита соответственно.

При условно неподвижном колесе 1 по принципу обращенного движения величина передаточного отношения от второго звена к водилу определяется по формуле

i_2h⁽¹⁾ =w₂/w_h=(r₂ – r₁)/ r₂=1– (r₁/ r₂)=1– i₂₁^(h), (2.134)

где i₂₁^(h) – передаточное отношение от второго колеса к первому при условно остановленном водиле h. В планетарных механизмах с круглыми колесами сумма передаточных отношений при различных останавливаемых звеньях всегда равна единице

i₂_h⁽¹⁾ + i₂₁⁽^h⁾=1. (2.135)

Сателлитные механизмы с двумя и более степенями подвижности называют

дифференциальными механизмами, (рисунок 2.32).

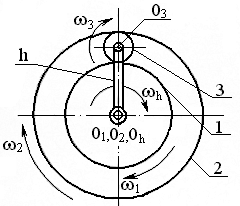
Рисунок 2.32 – Дифференциальный механизм с цилиндрическими

колесами: 1, 2 – колеса центральные; 3 – сателлит; h – водило

Классификационные формулы планетарных передач составляют с помощью букв латинского алфавита. Заглавными буквами обозначают типы механизмов, а строчными буквами обозначают звенья, образующие эти механизмы. Особенности структуры передачи уточняют индексами. Нижние индексы относятся к основным звеньям. Первый из них указывает звено, передающее наибольший крутящий момент. Верхний индекс указывает какое звено не вращается.

Планетарные зубчатые передачи классифицируют по сходным конструктивно – функциональным признакам механизмов.

Планетарный механизм 2k – h содержит в качестве основных звеньев два центральных колеса kи водило h. Передачи с этим механизмом имеют обозначения:

А – передача, механизм которой содержит одновенцовый сателлит, центральное колесо ас внешними зубьями и центральное колесо b с внутренними зубьями (рисунок 2.33, а – передача А^b_ha с остановленным центральным внешним колесом b; рисунок 2.33,б – передача А^а_hb c остановленным центральным внутренним колесом a; рисунок 2.33,в – передача А^h_ba с остановленным водилом h);

В – передача, механизм которой содержит двухвенцовый сателлит, центральное колесо а с внешними зубьями и центральное колесоb с зубьями на внутренней поверхности обода (рисунок 2.33, г – передача В^b_ha c остановленным внешним центральным колесом b);

С – передача, механизм которой содержит двухвенцовый сателлит и центральные колеса b и ес внутренними зубьями (рисунок 2.33,д – С^b_eh c остановленным внешним центральным колесом b);

Е – передача, механизм которой содержит одновенцовый сателлит и конические зубчатые колеса (рисунок 2.33, е – передача Е).

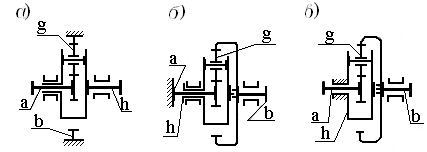
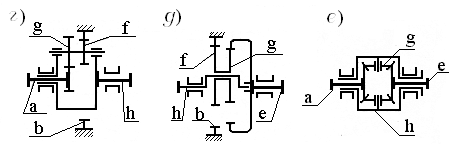
Рисунок 2.33– Схемы передач с механизмом 2k –h

Механизм 3k (рисунок 2.34) в качестве основных звеньев имеет три центральных колеса. В этом случае водило не воспринимает нагрузку от внешних моментов, а только поддерживает сателлиты.

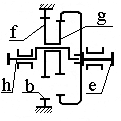
Рисунок 2.34 – Схема передачи с механизмом 3k

Замкнутые передачи (передачи g – d) содержат дифференциал, основные звенья которого обозначают буквами a, b, g. На рисунке 2.35,а показан механизм, у которого звено g вращается с одним из выходных валов, а два других основных звена a и b связаны с другим выходным валом d. На рисунке 2.35,б показан механизм основное звено b которого соединено с выходным валом d (передачей b– d), а механизм А (передача a– d) выполняет функции тихоходной ступени.

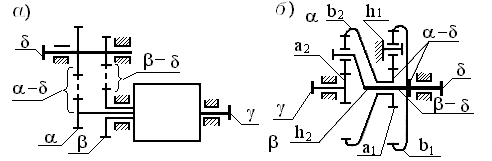
Рисунок 2.35 – Схемы передач с механизмом g - d

В обозначении последовательно соединенных механизмов применяют знак лигатуры     , который указывает пару звеньев соседних ступеней, соединенных друг с другом . Звеньям тихоходной ступени присваивают индекс 1, а звеньям быстроходной ступени – индекс 2 (A^b¹_h₁_a₁A^b²_h₂_a₂, A^b¹_h₁_a₁A^h²_b₂_a₂).

На рисунке 2.36 изображены схемы передач, составленных из двух механизмов А.

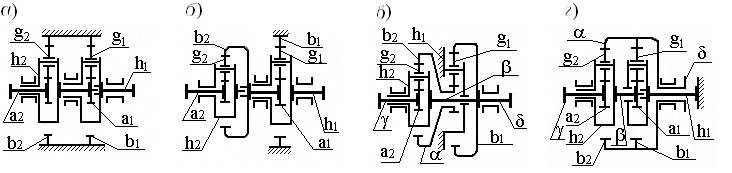
Рисунок 2.36 – Схемы двухступенчатых планетарных передач:

а) передача А^b¹_h₁_a₁А^b²_h₂_a₂; б) передача А^b¹_h₁_a₁А^h²_b₂_a₂;

в) передача (АА)^h¹₍_b₁_h₂₎_a₂; г) передача (АА)^h¹₍_b₁_b₂₎_a₂

При расчете зубчатым колесам помимо принятых буквенных обозначений присваются индексы 1 и 2, соответственно меньшему и большему элементу сцепляющейся пары.

Для установления величины усилий в зацеплении планетарных передач всех типов рассматривают равновесие каждого звена под действием внешних нагрузок.

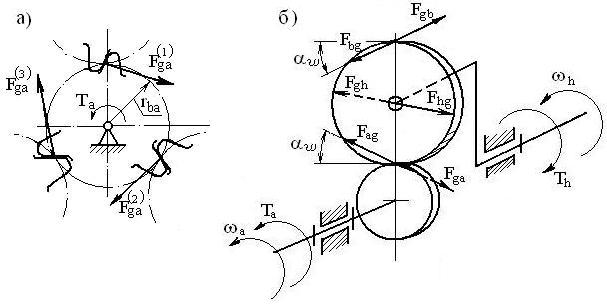
Рисунок 2.37 – Силы в планетарной зубчатой передаче:

a) – распределение усилий между колесами; б) – силы в зацеплении

( F⁽¹⁾_g_а, F⁽²⁾_g_а, F⁽³⁾_g_а–силы, действующие между сателлитом и центральным колесом а; F_gb – сила, действующая между сателлитом и центральным колесом b; Т_а, Т_h – моменты вращающие на центральном колесе и водиле соответственно; w_a, w_h – угловые скорости на центральном колесе и водиле соответственно; F_hg – сила, действующая между водилом и сателлитом)



Силы в зацеплении сателлита с центральным колесом рассчитывают с учетом коэффициента неравномерности нагрузки К_Н по наиболее нагруженному сателлиту. В расчетах опор сателлитов необходимо учитывать центробежную силу. Радиальные составляющие сил, действующих в передаче, которая имеет несколько сателлитов, не учитывают, т.к. они уравновешивают друг друга.

В трехсателлитной передаче (рисунок 2.37) вращающий момент Т_а на центральном колесе ауравновешивается силами F⁽¹⁾_g_а, F⁽²⁾_g_а, F⁽³⁾_g_а

                                                                  Т_а=r_ba×( F⁽¹⁾_g_а+F⁽²⁾_g_а+F⁽³⁾_g_а ,                         (2.136)

где r_ba – радиус основной окружности центрального колеса.

В идеальной передаче силы равны и нормальная сила от сателлита F_g_а

                                                                          F_g_а = Т_а/( r_ba×n_w).                                   (2.137)

В случае передачи с числом сателлитов n_w>3 неравномерность распределения нагрузки исключить не удается и это учитывается умножением силы F_g_а на коэффициент неравномерного распределения нагрузки К_Н. Участие сателлита одновременно в двух зацеплениях приводит к тому, что одновенцовый сателлит не передает вращающий момент и находится в равновесии под действием сил F_а_g, F_bg и F_hg со стороны колес a, bи водила hсоответственно.

Учитывая, что углы зацепления a_w одинаковы, из уравнения равновесия

                                                                          F_hg =2× F_а_g×К_Н×cos a_w.                             (2.138)

Сила F_hg необходима при расчете подшипника сателлита и оси водила. Нормальную силу F_n , приходящуюся на единицу длины контактной линии l, называют удельной нагрузкой

                    w_m=F_n/l.                                           (2.139)

Рабочая нагрузка равна произведению удельной нагрузки на корректирующие коэффициенты (коэффициенты режима нагружения, неравномерности распределения нагрузки, динамического влияния и т.п.), которые устанавливаются в каждом конкретном случае с учетом принятых критериев работоспособности. В расчетах оценивают нагрузку, которая вызывает наибольшее опасное напряжение для данного вида повреждения.