
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Степень с иррациональным и действительным показателем
Степень с иррациональным и действительным показателем
Известно, что множество действительных чисел можно рассматривать как объединение множеств рациональных и иррациональных чисел. Поэтому степень с действительным показателем можно будет считать определенной, когда будут определены степень с рациональным показателем и степень с иррациональным показателем. Про степень с рациональным показателем мы говорили в предыдущем пункте, осталось разобраться со степенью с иррациональным показателем.
К понятию степени числа a с иррациональным показателем 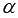 будем подходить постепенно.
будем подходить постепенно.
Пусть 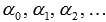 - последовательность десятичных приближений иррационального числа
- последовательность десятичных приближений иррационального числа 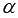 . Для примера возьмем иррациональное число
. Для примера возьмем иррациональное число 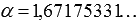 , тогда можно принять
, тогда можно принять 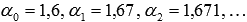 , или
, или 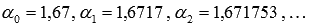 , и т.п. Здесь стоит отметить, что числа
, и т.п. Здесь стоит отметить, что числа 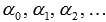 - рациональные.
- рациональные.
Последовательности рациональных чисел 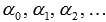 соответствует последовательность степеней
соответствует последовательность степеней 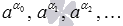 , причем мы можем вычислить значения этих степеней на базе материала статьи возведение в рациональную степень. В качестве примера возьмем a=3,
, причем мы можем вычислить значения этих степеней на базе материала статьи возведение в рациональную степень. В качестве примера возьмем a=3, 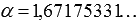 и
и 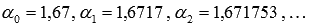 , тогда
, тогда 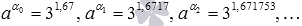 , а после возведения в степень получаем .
, а после возведения в степень получаем .
Наконец, последовательность 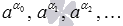 сходится к некоторому числу, которое и является значением степени числа a с иррациональным показателем
сходится к некоторому числу, которое и является значением степени числа a с иррациональным показателем 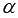 . Вернемся к нашему примеру: степень с иррациональным показателем вида
. Вернемся к нашему примеру: степень с иррациональным показателем вида 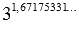 сходится к числу, которое с точностью до сотых равно 6,27.
сходится к числу, которое с точностью до сотых равно 6,27.
Определение.
Степенью положительного числа a с иррациональным показателем 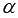 называют выражение
называют выражение 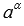 , значение которого равно пределу последовательности
, значение которого равно пределу последовательности 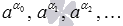 , где
, где 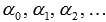 - последовательные десятичные приближения иррационального числа
- последовательные десятичные приближения иррационального числа 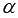 .
.
Степень числа нуль определяется для положительных иррациональных показателей, при этом 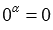 . Например,
. Например, 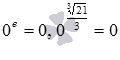 . А степень числа 0 с отрицательным иррациональным показателем не определяется, к примеру,
. А степень числа 0 с отрицательным иррациональным показателем не определяется, к примеру, 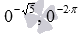 - не определены.
- не определены.
Отдельно стоит сказать про иррациональную степень единицы – единица в любой иррациональной степени равна 1. Например, 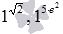 и
и 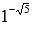 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|