
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулы сокращённого умножения.
Руководство по решению задач к занятию 1.
Формулы сокращённого умножения.
При возведении двучлена в степень, умножении многочленов, разложении их на множители и других тождественных преобразованиях многочленов применяются специальные формулы, которые называются формулами сокращенного умножения.
1) (a + b)  = a
= a  + 2ab + b
+ 2ab + b  ;
;
2) (a - b)  = a
= a  - 2ab + b
- 2ab + b  ;
;
3) a  - b
- b  = (a – b) (a + b) ;
= (a – b) (a + b) ;
4) (a + b) 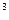 = a
= a 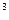 + 3a
+ 3a  b + 3ab
b + 3ab  + b
+ b 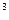 ;
;
5) (a - b) 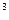 = a
= a 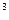 - 3a
- 3a  b + 3ab
b + 3ab  - b
- b 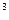 ;
;
6) a 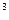 - b
- b 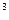 = (a – b)( a
= (a – b)( a  + ab + b
+ ab + b  );
);
7) a 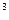 + b
+ b 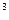 = (a + b)( a
= (a + b)( a  - ab + b
- ab + b  );
);
Устно эти формулы произносятся следующим образом:
1) квадрат суммы двух чисел равен сумме квадратов этих чисел, сложенной с их удвоенным произведением;
2) разность квадратов двух чисел равна произведению разности этих чисел на их сумму;
3) разность кубов двух чисел равно разности этих чисел, умноженной на неполный квадрат их суммы ( выражение a  + ab + b
+ ab + b  называется неполным квадратом суммы двух чисел, а выражение a
называется неполным квадратом суммы двух чисел, а выражение a  - ab + b
- ab + b  - неполным квадратом разности).
- неполным квадратом разности).
Пример 1. Устно умножить 41 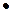 39.
39.
41 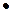 39 = (40 + 1)(40 – 1) = 40
39 = (40 + 1)(40 – 1) = 40  - 1
- 1  = 1599
= 1599
Пример 2.Устно вычислить 49  .
.
49  =(50 – 1)
=(50 – 1)  = 50
= 50  - 2
- 2 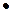 50 + 1 = 2500 – 100 + 1 = 2401
50 + 1 = 2500 – 100 + 1 = 2401
Пример 3.Преобразовать выражение
(1 – a)(1 - a + a  )(1 + a + a
)(1 + a + a  )(1 + a)
)(1 + a)
Произведение первой скобки на третью – это произведение разности чисел 1 и a на неполный квадрат их суммы, т.е. можно применить формулу разности кубов (формула 6):
(1 – a)(1 + a + a  ) = 1
) = 1 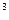 - a
- a 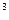 .
.
Произведение четвертого сомножителя и второго равно сумме кубов чисел 1 и a (формула 7). Следовательно,
(1 – a)(1 - a + a  )(1 + a + a
)(1 + a + a  )(1 + a) = (1 - a
)(1 + a) = (1 - a 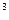 )(1 + a
)(1 + a 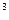 ).
).
Произведение разности чисел 1 и a 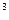 на их же сумму равно разности квадратов этих чисел (формула 3):
на их же сумму равно разности квадратов этих чисел (формула 3):
(1 - a 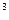 )(1 + a
)(1 + a 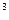 ) = 1 – (a
) = 1 – (a 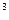 )
)  = 1 - a
= 1 - a 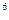 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|