Тема: Действительные числа. Множества.

Тема: Действительные числа. Множества.

Дата: 20.10.2020 г.

Группа: ПЦ-265

Студенты должны знать: Понятие множества натуральных, целых, рациональных и действительных чисел

Студенты должны уметь: проводить сравнительный анализ полученного результата, пользоваться умением самопроверки, реализовывать всевозможные способы работы с разнообразием чисел.

1.Актуализация опорных знаний

Устный опрос:

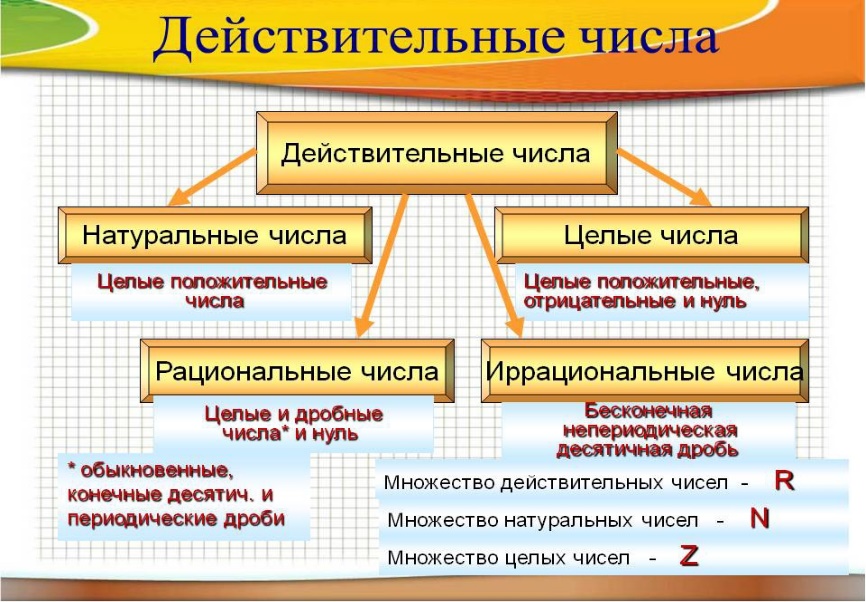
1. Какие числа наз. натуральными?

2. Какие числа наз. целыми?

3. Какие числа наз. рациональными?

4. Какие числа наз. иррациональными?

5. Какие числа наз. действительными?

1.Изучение новой темы.

[а;в] – отрезок – множество всех действительных чисел х, удовлетворяющих двойному неравенству а ≤ х ≤ в . Точки а и в называются концами отрезка и принадлежат этому отрезку.

(а;в) – интервал - множество всех действительных чисел х, удовлетворяющих двойному неравенству а

[а;в) – полуинтервал - множество всех действительных чисел х, удовлетворяющих двойному неравенству а ≤ х

(а;в] - полуинтервал - множество всех действительных чисел х, удовлетворяющих двойному неравенству а

Множество не содержащее ни одного элемента, называют пустым множеством. Его обозначают знаком Ø.

Тот факт, число принадлежит или не принадлежит множеству чисел, записывают с помощью определенных знаков: - принадлежит, - не принадлежит.

Объединением множеств А и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Обозначают А U В.

Пересечением множеств А и В называют множество, состоящее из всех элементов, каждый из которых принадлежит и множеству А, и множеству В. Обозначается А В.

Если любой элемент множества А является элементом множества В, то А называют подмножеством множества В. Пишут А В и говорят «А – подмножество В».

12 Следующая ⇒