
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
МДК .03.01 Геодезия с основами картографии и картографического черчения
МДК .03.01 Геодезия с основами картографии и картографического черчения
Лекция на тему : Прямая и обратная геодезическая задачи.
Преподаватель Завязкина Л.С.
Прямая и обратная геодезические задачи
а) Прямая геодезическая задача
Прямая геодезическая задача заключается в том, что если известны координаты Х и У начальной точки направления , дирекционный угол направления α и длина направления d, ТО можно определить координаты конечной точки направления

Прямая геодезическая задача
Дано:
координаты точки 1 - х1, У1;
горизонтальное проложение линии 1 – 2 - d1-2;
дирекционный угол линии 1 – 2: α1-2 ,
Найти: координаты точки 2: х2, у2.
Решение:
координаты точки 2:
х2 = х1 + ∆х; у2 = у1 + ∆у,
где приращения координат ∆х = d · cos α; у = d · sin α,
откуда х2 = х1 + d · cos a; у2 = у1 + d · sin a.
Знаки приращений координат ∆х и ∆у зависят от знаков функций sin a и cos a.
б) Обратная геодезическая задача
Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между точками и дирекционный угол направления

|
Обратная геодезическая задача
Дано: координаты точек 1 и 2: х1, у1; х2, у2
Найти: горизонтальное проложение линии 1 – 2: d1-2 ;
дирекционный угол линии 1 – 2: α1-2.
Решение: ∆х = х2 – х1; ∆у = у2– у1;
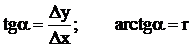 ;
;
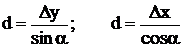 .
.
По значению tg a определяется румб линии.
По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
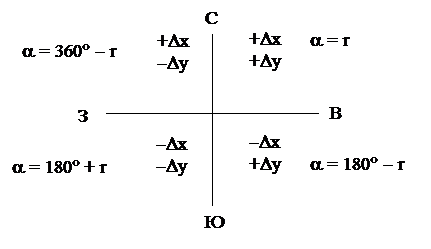
Знаки приращений координат
в зависимости от четверти
https://www.mozgan.ru/Table/TableBradis
Задание :
Доказать прямую и обратную геодезические задачи, знать формулы и в чем заключается прямая и обратная геодезические задачи.
Обратная связь:
Тел :8916-857-70-96;
lyubov.zavyazkina@gmail.com
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|