
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные свойства функции.
Основные свойства функции
Определение : Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число y.
Обозначение:
y = f(x),
где x – независимая переменная (аргумент), y – зависимая переменная (функция). Множество значений x называется областью определения функции (обозначается D(f)). Множество значений y называется областью значений функции (обозначается E(f)). Графиком функции называется множество точек плоскости с координатами (x, f(x))
Способы задания функции.
1. аналитический способ (с помощью математической формулы);
2. табличный способ (с помощью таблицы);
3. описательный способ (с помощью словесного описания);
4. графический способ (с помощью графика).
Основные свойства функции.
1. Четность и нечетность
Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)
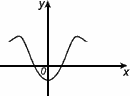
График четной функции симметричен относительно оси 0y
Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)
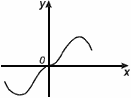
График нечетной функции симметричен относительно начала координат.
2.Периодичность
Функция f(x) называется периодической с периодом 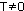 , если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).
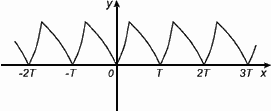
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.
3. Монотонность (возрастание, убывание)
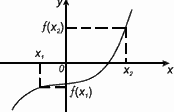
Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).
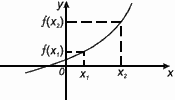
Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).
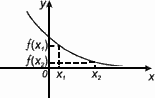
4. Экстремумы
Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х) 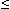 f(Xmax).
f(Xmax).
Значение Ymax=f(Xmax) называется максимумом этой функции.
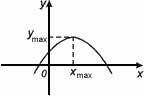
Хmax – точка максимума
Уmax – максимум
Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х) 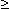 f(Xmin).
f(Xmin).
Значение Ymin=f(Xmin) называется минимумом этой функции.
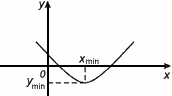
Xmin – точка минимума
Ymin – минимум
Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.
5. Нули функции
Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.
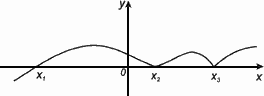
Х1,Х2,Х3 – нули функции y = f(x).
Задачи и тесты по теме "Основные свойства функции"
· Свойства функций - Числовые функции 9 класс
· Свойства логарифмов - Показательная и логарифмическая функции 11 класс
· Функция квадратного корня, его свойства и график - Функция квадратного корня. Свойства квадратного корня 8 класс
· Степенные функции, их свойства и графики - Степени и корни. Степенные функции 11 класс
· Показательная функция, её свойства и график - Показательная и логарифмическая функции 11 класс
Рекомендации к теме
Изучив эту тему, Вы должны уметь находить область определения различных функций, определять с помощью графиков промежутки монотонности функции, исследовать функции на четность и нечетность. Рассмотрим решение подобных задач на следующих примерах.
Примеры.
1. Найти область определения функции.
a) 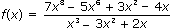
Решение: область определения функции находится из условия
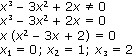
Ответ: 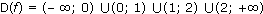
б) 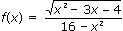
Решение: область определения функции находится из условий

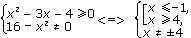
Ответ: 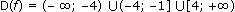
2. Исследовать на четность и нечетность функцию:
a) 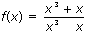
Решение:
| 1) | 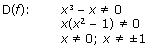
|
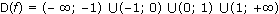 - симметрична относительно нуля.
- симметрична относительно нуля.
| 2) | 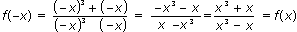
|
следовательно, функция f(x) – четная.
Ответ: четная.
в) 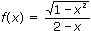
1) 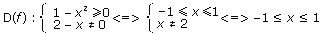
D(f) = [-1; 1] – симметрична относительно нуля.
| 2) | 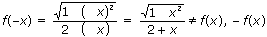
|
следовательно, функция не является ни четной, ни нечетной.
Ответ: ни четная, ни не четная.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|