
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 3.
Стр 1 из 3Следующая ⇒
| Примеры решения задач по теме «Определители» |
Задача 1.
Вычислить определитель
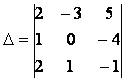 .
Указание
Воспользуйтесь либо правилом треугольников, либо разложением определителя по 2-й строке или 2-му столбцу, содержащим нулевой элемент.
Решение
1-й способ (правило треугольников).
Вычислим определитель 3-го порядка, используя его определение:
Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 - 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =
= 0 + 24 + 5 – 0 + 8 – 3 = 34.
2-й способ (разложение по строке).
Применим свойство определителя: .
Указание
Воспользуйтесь либо правилом треугольников, либо разложением определителя по 2-й строке или 2-му столбцу, содержащим нулевой элемент.
Решение
1-й способ (правило треугольников).
Вычислим определитель 3-го порядка, используя его определение:
Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 - 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =
= 0 + 24 + 5 – 0 + 8 – 3 = 34.
2-й способ (разложение по строке).
Применим свойство определителя:
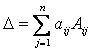 .
Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (А22 = 0), поскольку при этом нет необходимости находить А22, так как произведение А22 А22 = 0. Итак, .
Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (А22 = 0), поскольку при этом нет необходимости находить А22, так как произведение А22 А22 = 0. Итак,
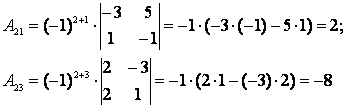 (напомним, что определитель второго порядка, входящий в алгебраическое дополнение Aij, получается вычеркиванием из исходного определителя I-й строки и J-го столбца).
Тогда Δ = А21 А21 + А23 А23 = 1·2 + (-4)(-8) = 34.
Ответ: Δ = 34.
Задача 2.
Используя свойства определителя, вычислить определитель
(напомним, что определитель второго порядка, входящий в алгебраическое дополнение Aij, получается вычеркиванием из исходного определителя I-й строки и J-го столбца).
Тогда Δ = А21 А21 + А23 А23 = 1·2 + (-4)(-8) = 34.
Ответ: Δ = 34.
Задача 2.
Используя свойства определителя, вычислить определитель
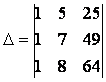 .
Указание
Вычитая из 2-й и 3-й строк определителя соответствующие элементы 1-й строки, добьемся того, что в 1-м столбце останется только один ненулевой элемент. Далее можно разложить определитель по 1-му столбцу.
Решение
Поскольку все элементы первого столбца равны 1, вычтем из 2-й и 3-й строк определителя соответствующие элементы 1-й строки (при этом величина определителя не изменится – свойство 6): .
Указание
Вычитая из 2-й и 3-й строк определителя соответствующие элементы 1-й строки, добьемся того, что в 1-м столбце останется только один ненулевой элемент. Далее можно разложить определитель по 1-му столбцу.
Решение
Поскольку все элементы первого столбца равны 1, вычтем из 2-й и 3-й строк определителя соответствующие элементы 1-й строки (при этом величина определителя не изменится – свойство 6):
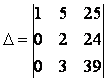 .
Заметим, что теперь все элементы 2-й строки кратны двум, а элементы 3-й строки кратны трем. По следствию 2.2 соответствующие множители можно вынести за знак определителя: .
Заметим, что теперь все элементы 2-й строки кратны двум, а элементы 3-й строки кратны трем. По следствию 2.2 соответствующие множители можно вынести за знак определителя:
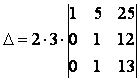 .
Вычтем из элементов 3-й строки полученного определителя соответствующие элементы 2-й строки: .
Вычтем из элементов 3-й строки полученного определителя соответствующие элементы 2-й строки:
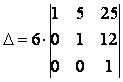 И разложим определитель по 1-му столбцу:
И разложим определитель по 1-му столбцу:
 Ответ: Δ = 6.
Ответ: Δ = 6.
|
Задача 3.
Используя свойства определителей, вычислить определитель
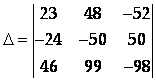 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|