Практическое занятие №1

Практическое занятие №1

Тема: Определение погрешности измерительного прибора

Цель работы: научиться определять погрешности измерительного прибора;

- определять метрологические характеристики средств измерения;

Перед началом занятия необходимо знать: Средства измерений: меры, измерительные приборы, измерительные системы. Точность средств измерений. Погрешности измерений: систематические, случайные, грубые.

После окончания занятия необходимо уметь: определять погрешности измерительного прибора

Теория:

Погрешности могут быть:

• систематические,

Систематической погрешностью называется составляющая суммарной погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.

Систематические погрешности:

· не зависят от числа измерений;

· искажения, вносимые ими в результат измерения, поддаются исключению или учету;

· могут быть определены в большинстве случаев путем эксперимента;

· иногда их можно определить путем вычислений на основании характеристик СИ, используемых в измерениях.

В ряде случаев систематическая погрешность может быть исключена в процессе измерений; при этом процесс нахождения исправленного значения измеряемой ФВ может осуществляться и без определения значения систематической погрешности (если это сделать затруднительно или невозможно) — устраняется причина, вызывающая появление погрешности.

Таким образом, систематическая погрешность представляет собой определенную (неслучайную) функцию неслучайных факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, а также условий их применения.

Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру поведения.

*В зависимости от причин возникновения рассматривают пять видов систематических погрешностей:

1. погрешности метода или теоретические погрешности;

2. инструментальные погрешности;

3. погрешности, возникающие в результате неправильной установки СИ;

4. погрешности, возникающие из-за влияния внешних условий;

5. субъективные (личные) погрешности.

• случайные,

Случайная погрешность -составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях.

• грубые,

как правило, допускаются самим исполнителем, который из-за неопытности или усталости неправильно считывает показания прибора или ошибается при обработке информации. Их причиной могут стать и неисправность средств измерений, и резкое изменение условий измерения.

Полностью исключить погрешности практически невозможно, а вот установить пределы возможных погрешностей измерения и, следовательно, точность их выполнения необходимо.

Погрешностью измерения 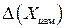называют отклонение результата измерения (X) от истинного или действительного значения

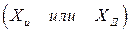измеряемой величины:

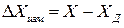
Погрешность может быть абсолютной, относительной и приведенной.

Абсолютная погрешность измерения 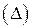представляет собой разность между измеренной величиной и истинным или действительным значением этой величины, т. е.

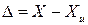или .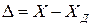

Относительная погрешность измерения 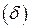представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины. Относительная погрешность может выражаться в долях,

тогда ,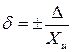

или в процентах,

тогда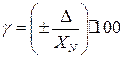

Приведенная погрешность измерения (у) представляет собой отношение абсолютной погрешности к нормированному значению величины, например, ее максимальному значению,

т. е. ,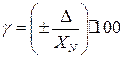

где 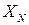нормированное значение величины,

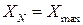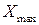( — максимальное значение измеряемой величины). При многократных измерениях в качестве истинного значения, как правило, используют среднее арифметическое значение:

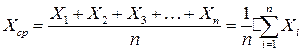
В отличие от относительной и приведенной абсолютная погрешность всегда имеет ту же размерность, что и измеряемая величина.

Величина X, полученная в одной серии измерений, является случайным приближением к 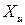. Для оценки ее возможных отклонений от 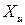определяют среднее квадратическое отклонение:

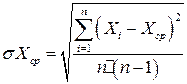
Для оценки рассеяния отдельных результатов измерения 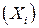относительно среднего арифметического значения 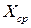определяют среднеквадратическое отклонение:

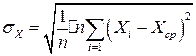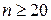при или

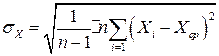при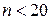

Применение формул правомерно при условии постоянства измеряемой величины в процессе измерения. Если при измерении величина изменяется, как, например, при измерении потенциала проводника через равные отрезки длины, то в формулах в качестве 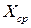следует брать какую-то постоянную величину, например, начало отсчета.

Формулы соответствуют центральной предельной теореме теории вероятностей, согласно которой

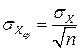
Поправка – значение величины, вводимое в неисправленный

результат измерения с целью исключения составляющих систематической погрешности. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Дидактическое обеспечение: Варианты заданий.

Исходные данные: таблица1; .

12 Следующая ⇒