Задание 2 на неделю с 28 сентября

Задание 2 на неделю с 28 сентября

Задание 3 на неделю с 5 октября

Задание 4 на неделю с 12 октября

Пояснения к заданию 2.

2.1.

Второе уравнение в системе умножить на 10. Затем решить подстановкой или сложением.

2.2.

Разложить на множители х²- 49 по формуле ФСУ и разложить х²+ 4х – 21 на множители ( ах² +вх+с= а ( х-х₁)(х- х₂)). Затем вынести за скобку общий множитель. Далее упростить и вспомнить когда произведение равно 0.

2.3. Вспомнить свойства степени.

2.4.

Первое неравенство – дробно- рациональное, решается методом интервалов. Второе линейное. Затем находим общее решение ( на одной оси или на объединяя две оси).

2.5.

Перенести всё в одну часть и разложить по формуле а²-в² = ( а-в)(а+в). Далее упростить выражения в скобках и решить методом интервалов.

Пояснения к заданию 3.

3.1 Попробуйте решить задачу аналогично, но подумайте как найти скорость поезда относительно пешехода. И переведите скорость в метры /минуту, а 30 сек. В минуты.

3.2.

Составьте и заполните таблицу: за час; кол-во часов; всего. Составьте уравнение.

3.3. Проанализируйте решение задачи ниже:

Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?

Решение.

Свежие фрукты содержат 20% питательного вещества, а высушенные — 72%. В 288 кг свежих фруктов содержится 0,2 · 288 = 57,6 кг питательного вещества. Такое количество питательного вещества будет содержаться в 57,6 :0,72 кг высушенных фруктов.

Ответ: 80 кг.

3.4. Разберите решение аналогичной задачи.

Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?

Решение.

Пусть концентрация первого раствора — х, концентрация второго раствора — y. Составим систему уравнений согласно условию задачи и решим ее:

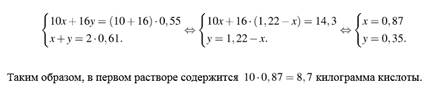
Ответ: 8,7.