Вопросы к коллоквиуму по математическому анализу по теме

Вопросы к коллоквиуму по математическому анализу по теме

«Теория пределов и непрерывности функции».

Часть 1 «Предел числовой последовательности»

1. Определение числовой последовательности и ее предела, геометрическая интерпретация предела.

Теорема об ограниченности сходящейся числовой последовательности.
Теорема о пределе суммы числовых последовательностей.
Теорема о пределе разности числовых последовательностей.
Теорема о пределе произведения числовых последовательностей.
Теорема о пределе частного числовых последовательностей.
Теорема о предельном переходе в неравенствах.
Бесконечно большие и бесконечно малые последовательности. Связь между ними. Свойства бесконечно малых последовательностей.
Теорема о пределе монотонно возрастающей числовой последовательности.
Теорема о пределе монотонно убывающей числовой последовательности.
Доказать, что последовательность 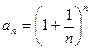имеет предел.
Доказать, что , , , .
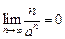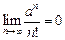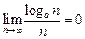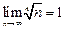Фундаментальные последовательности. Критерий Коши.
Подпоследовательности и частичные пределы. Условие расходимости последовательности.

Часть 2 «Предел функции»

Определения предела функции по Коши и по Гейне. Теорема об эквивалентности двух определений предела функции (без доказательства).
Односторонние пределы. Необходимое и достаточное условие существования предела функции.
Первый замечательный предел.
Второй замечательный предел.
Сравнение бесконечно малых величин. Определение порядка малости бесконечно малой и выделение главной части бесконечно малой.
Теорема о вычислении пределов с помощью таблицы эквивалентных бесконечно малых. Таблица эквивалентных бесконечно малых.
Сравнение бесконечно больших величин. Определение порядка роста бесконечно большой и выделение главной части бесконечно большой.
Записать на языке "ε-δ" определения пределов функции с примерами графиков

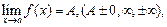
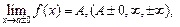
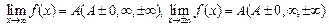
(этот вопрос рассматривается на практическом занятии 6, смотрите в тетради по практике)

Часть 3 «Непрерывность функции»

1. Непрерывность функции в точке, одностороння непрерывность. Необходимое и достаточное условие непрерывности функции в точке.

2. Классификация точек разрыва.

3. Непрерывность функций на множестве, непрерывность элементарных функций, сложной и обратной функции.

4. Первая и вторая теоремы Коши для непрерывных функций.

5. Первая и вторая теоремы Вейерштрасса для непрерывных функций.