Урок 5. Работа и энергия. Законы сохранения.

Урок 5. Работа и энергия. Законы сохранения.

Домашнее задание: 2.40, 2.44, 2.47, 2.53, 2.63, 2.67, 2.73, 2.77, 2.89, 2.102

Теорию кратко конспектируем в тетрадь и записываем разобранные задачи. Высылаете мне фото дом. задания вместе с классной работой!!!

Импульс. Произведение массы точки на ее скорость называют импульсом

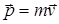Импульс системы материальных точек равен сумме импульсов точек

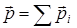Скорость изменения импульса системы точек равна сумме всех внешних действующих сил

, .

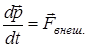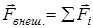Изменение импульса системы точек равно импульсу всех внешних сил

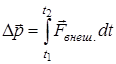Закон сохранения импульса: импульс замкнутой системы сохраняется

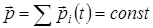Система называется замкнутой, если на нее не действуют внешние тела.

Центром масс системы называется точка, радиус-вектор которой определяется выражение

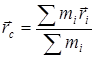Теорема о движении центра масс: центр масс системы движется как материальная точка, к которой приложены все действующие на систему силы и в которой сосредоточена вся масса системы

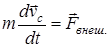На практике широко используют следующие следствия баланса импульса:

если действующие на систему силы скомпенсированы, то импульс системы сохраняется

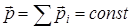, если ;

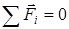если проекция сил на ось х равна нулю, то проекция импульса системы на эту ось сохраняется

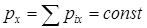, если .

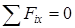Работа и энергия. Элементарной работой силы 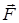при перемещении 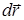называется скалярное произведение силы на перемещение

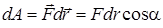Работа силы при перемещении из точки 1 в 2 определяется интегралом

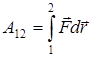Работа силы за единицу времени называется мощностью

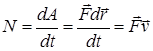Кинетическая энергия точки и системы точек определяется по формулам

, .

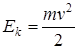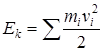Изменение кинетической энергии системы равно сумме работ всех сил

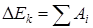Среди сил в механике выделяют консервативные, работа которых не зависит от формы траектории (тяжести, упругости и т.д.). Для консервативных сил вводится потенциальная энергия, убыль которой равна работе этих сил

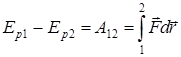Потенциальная энергия для сил тяжести и упругости равна

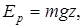
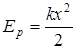где z – вертикальная координата, х – деформация пружины.

Проекция силы на ось х и потенциальная энергия связаны выражением

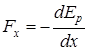Полной механической энергией называется сумма кинетической и потенциальной энергий системы

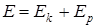Закон сохранения полной механической энергии: в замкнутой системе полная механическая энергия сохраняется при отсутствии сил трения

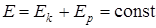, если .

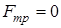Изменение полной механической энергии незамкнутой системы равно работе внутренних диссипативных 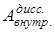и внешних 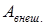сил

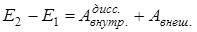Задача 1.С высокого берега в горизонтальном направлении со скоростью 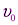брошена граната. Спустя время 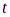граната разрывается на два осколка, массы которых и 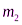, причем 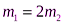. Первый осколок летит вертикально вниз, а второй – горизонтально. Определим скорости осколков после разрыва гранаты.

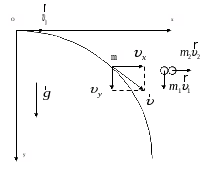
Учитывая быстротечность разрыва гранаты воспользуемся законом сохранения импульса: .

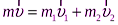
В проекциях на оси:

Oy: ;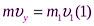

Ох: .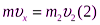

С учетом данных задачи .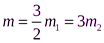

Проекции скорости гранаты 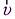на горизонтальную оси:

Ох: ;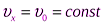

Oy: .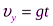

Тогда скорость осколка массой из (1) равна: 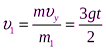; а осколка массой 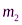из (2): .

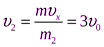Задача 2.Одной из интересных задач по теме «Законы сохранения в механике» является взаимодействие движущегося со скоростью 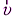шарика массой 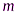с движущейся навстречу (или в одном направлении с шариком) со скоростью 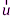массивной плиты массой М ( ).

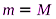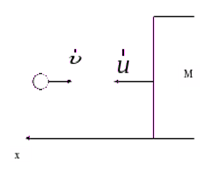В этой задаче рассматривается центральное упругое соударение, для которого справедливы законы сохранения импульса: ,

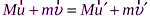или в проекции на ось Ох: 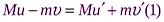, где и – скорости плиты и шарика после взаимодействия;

и энергии: .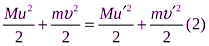

Приведем выражения (1) и (2) к следующему виду:

;

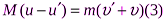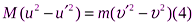Поделив выражения (4) и (3) почленно получаем: .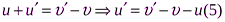

Подставим (5) в (1): 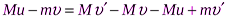, получаем

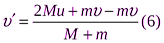
Разделим числитель и знаменатель на массу плиты М, учтем, что масса шарика 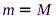, получим скорость шарика после взаимодействия с плитой

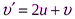Если шарик и плита движутся в одном направлении, то выражение (3) будет иметь вид: 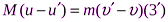. После деления выражений (4) и (3') почленно, получим: .

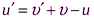Тогда 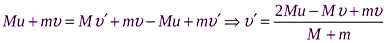. С учетом, что 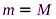, получаем скорость шарика после взаимодействия с плитой .

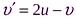Задача 3. Камень массой m = 0,2 кг бросили под углом α = 60˚ к горизонту со скоростью v₀ = 15 м/с. Найти кинетическую 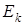, потенциальную 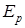и полную энергию 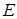камня спустя время t = 1 с после начала движения и в высшей точке траектории. Сопротивлением воздуха пренебречь.

Решение. При движении камня без сопротивления воздуха полная механическая энергия сохраняется, а его траектория будет параболой (рис. 1.8). Проекции скорости на горизонтальную и вертикальную оси х и у координат и координаты камня при таком движении изменяются по закону

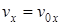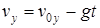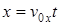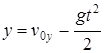, , , , (1)

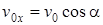где и 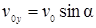– начальные значения скорости.

Кинетическую, потенциальную и полную энергию камня можно рассчитать по формулам

, , ,

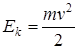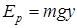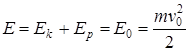где 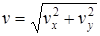– текущая скорость камня.

Для момента времени 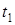= 1 с в точке М₁имеем:

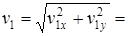8,15 м/с, 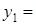8,1 м,

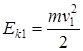= 6,5 Дж, 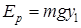= 16 Дж, 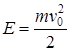= 22,5 Дж.

В верхней точке М₂траектории 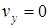и из второго уравнения (1) найдем время 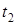подъема камня

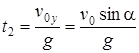= 1,3 с.

Высоту подъемаh камня определим по формуле

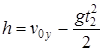= 8,4 м.

Кинетическую и потенциальную энергию в точке М₂рассчитаем по формулам

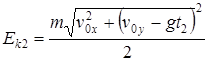= 5,6 Дж, 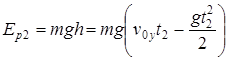= 16,9 Дж.

Задача 4. Человек массой m₁ = 60 кг, бегущий со скоростью v₁ = 8 км/ч, догоняет тележку массой m₂ = 80 кг, движущуюся со скоростью v₂ = 2,9 км/ч, и вскакивает в неё. С какой скоростью u станет двигаться тележка? С какой скоростью u¢ будет двигаться тележка, если человек бежал ей на встречу?

Решение. В данной задаче система «человек-тележка» не замкнута, но проекция внешних сил (тяжести и реакции опоры) на горизонтальное направление равна нулю, поэтому проекция импульса на это направление сохраняется. Значит для решения воспользуемся законом сохранения импульса.

В первом случае, когда человек догоняет тележку. По закону сохранения импульса, учитывая, что скорость человека и тележки после запрыгивания человека на тележку равны, имеем

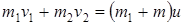Откуда находим скорость тележки с человеком

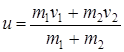= 5,14 км/ч.

Во втором случае, когда человек бежит навстречу тележке, по закону сохранения импульса с учетом направления движения, имеем

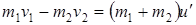Откуда находим скорость тележки с человеком

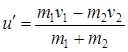= 1,71 км/ч.

Задача 5. Какую мощность N развивает двигатель автомобиля массой m = 1 т, если известно, что автомобиль едет с постоянной скоростью v = 36 км/ч: а) по горизонтальной дороге; б) в гору с уклоном 5 м на каждые 100 м пути; в) под гору с тем же уклоном? Коэффициент трения m = 0,07.

Решение. Как известно, мощность равна отношению работы 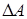ко времени 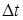, за которое совершена работа, и ее можно определить по формуле

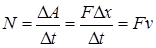где F – действующая на тело сила, 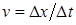- скорость тела.

Выразим силу F для всех случаев из второго закона Ньютона.

а) Так как v = const, то сила тяги автомобиля F скомпенсирована силой трения 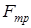, которая по закону трения 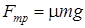, т.е. 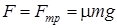. Следовательно, при движении автомобиля по горизонтальной дороге мощность равна

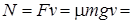6,9 кВт.

б) При движении в гору сила тяги двигателя противодействует скатывающей силе 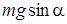и силе трения 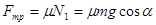, где a - угол наклона горы к горизонту, который найдем по формуле 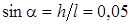. Следовательно, 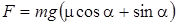. Тогда для мощности получим

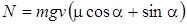= 11,8 кВт.

в) При движении под гору скатывающая сила будет направлена по направлению силы тяги, а сила трения против движения. Поэтому сила тяги будет равна 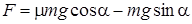. Мощность найдем по формуле

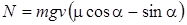= 2 кВт.