
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача1. Задача 2. Задача 3. Задача 4. Задача 5.
Семинар 3 
Волновая функция и её свойства. Стационарное уравнение Шредингера.
В квантовой механике состояние микрочастицы задают волновой функцией, квадрат модуля которой определяет вероятность того, что частица будет обнаружена в пределах бесконечно малого объёма:
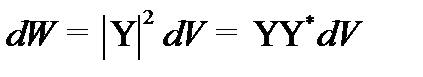
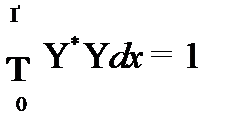 - условие нормировка означает, что вероятность нахождения частицы в рассматриваемом объёме равна единице, т. Е. она точно в этом объёме есть.
- условие нормировка означает, что вероятность нахождения частицы в рассматриваемом объёме равна единице, т. Е. она точно в этом объёме есть.
Волновые функции, удовлетворяющие этому условию, называются нормированными.
1.Волновая функция должна быть однозначной, непрерывной и конечной во всех точках пространства.
2.Первая производная от волновой функции тоже должна быть непрерывной и конечной во всех точках объёма.
Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики.
В отсутствие силового поля (частица свободна) оно имеет вид:
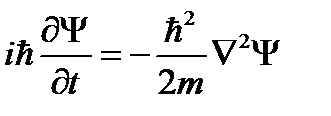 ;
;
для стационарных состояний:
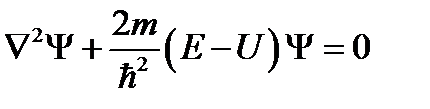
Если средние значения всех физических величин, характеризующих состояние микрочастицы, не зависят от времени, состояние называется стационарным,
Основным состоянием называется состояние, описываемое волновой функцией, которая соответствует наименьшему значению энергии
Уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям только при некоторых значениях энергии, называемых собственными.
Задача1
Состояние частицы описывается волновой функцией вида:
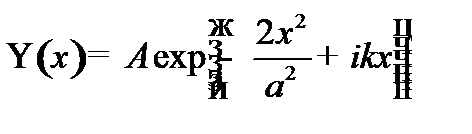 ; где
; где 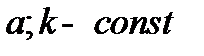 >0.
>0.
Найти:
- нормировочный коэффициент А;
- среднее значение координаты <x> в области x > a.
Решение:
1.Для нахождения нормировочного коэффициента используем условие нормировки: 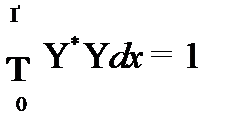 ,
,
(Здесь надо вспомнить физический смысл условия нормировки).
где 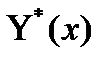 - комплексно сопряженная функция по отношению к волновой функции
- комплексно сопряженная функция по отношению к волновой функции
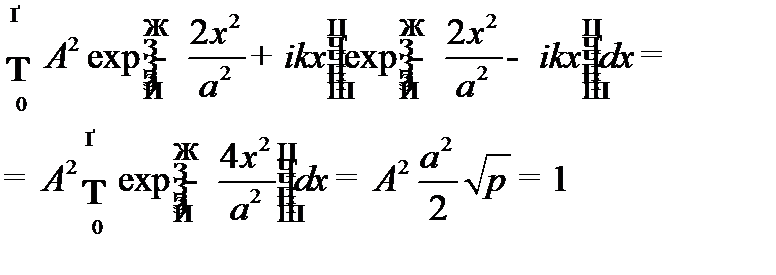
Для решения данного интеграла нужно использовать табличный интеграл (эти интегралы можно найти в методическом пособии по р6ешению задач «Квантовая физика. Элементы физики твердого тела и ядерной физики. Практический курс.» МартыненкоТ.П. Одинцова Г.А. и др) :
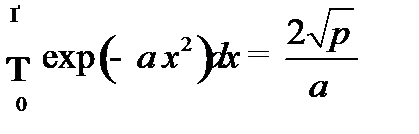
В данной задаче 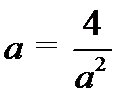
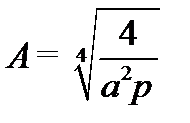 ;
;
2. Среднее значение х определяется выражением:
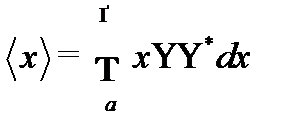
Пределы интегрирования определены условием задачи: от a до  .
.
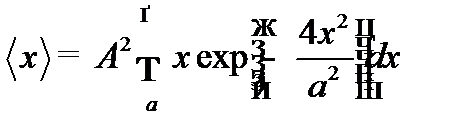
Заменим переменную: 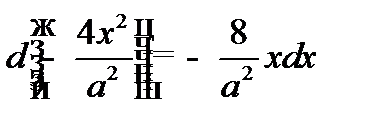
Умножим и разделим интеграл на 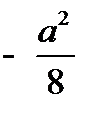 ;
;
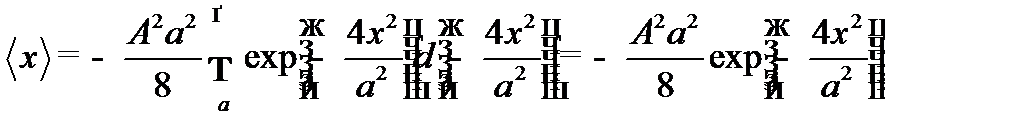
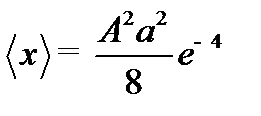
Подставив А, получим:
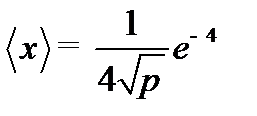
Задача 2
Волновая функция для частицы, находящейся в одномерной потенциальной яме шириной 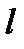 , имеет вид:
, имеет вид:
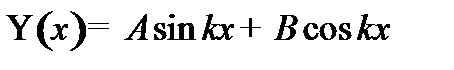 .
.
Найти нормированные волновые функции, удовлетворяющие граничным условиям: 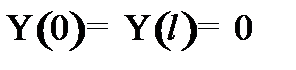
Задачу 2 попробовать решить самостоятельно.
Задача 3
Найти решение стационарного уравнения Шрёдингера для свободной частицы массой mв бесконечно глубокой потенциальной яме с абсолютно непроницаемыми стенками. Найти разность энергий между соседними разрешенными уровнями 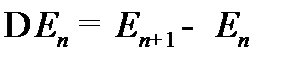 .
.
Решение:
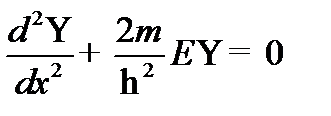
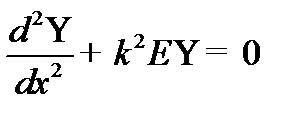
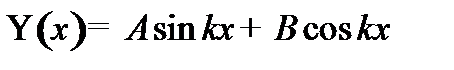
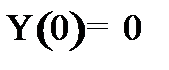
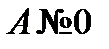
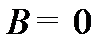
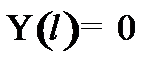
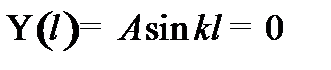
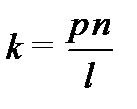
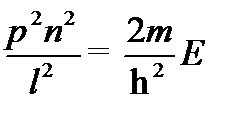
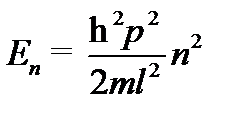
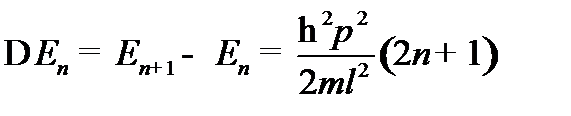
Из условия нормировки найдём А - 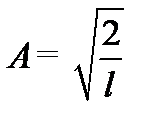
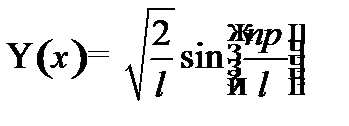
Задача 4
Частица массой m находится в одномерной потенциальной яме шириной l с абсолютно непроницаемыми стенками. Найти число энергетических уровней в интервале энергий 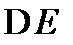
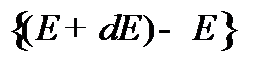 , если Е значительно больше основного состояния.
, если Е значительно больше основного состояния.
Задачу 4 попробовать решить самостоятельно.
Задача 5.
Частица находится в состоянии, которое описывается волновой функцией вида: 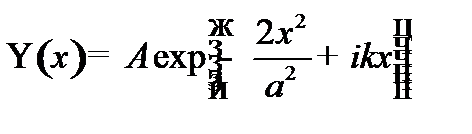 , где А; а; к >0.
, где А; а; к >0.
1. Найти распределение плотности вероятности нахождения частицы (построить график);
2. Эффективный размер области локализации частицы 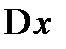 .
.
Решение:
1. Найдем распределение плотности вероятности нахождения частицы

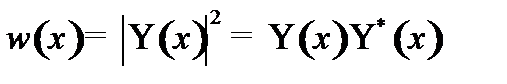
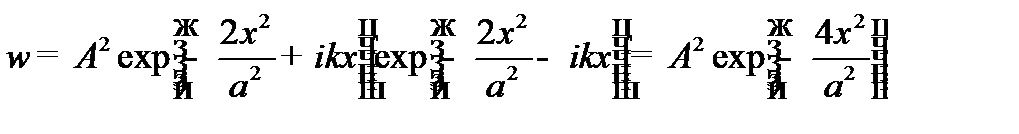 .
.
Из условия нормировки находим множитель A
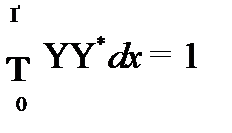
Для решения данного интеграла использовать табличный интеграл:
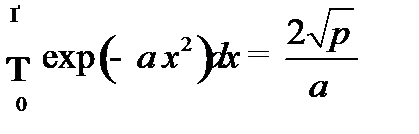
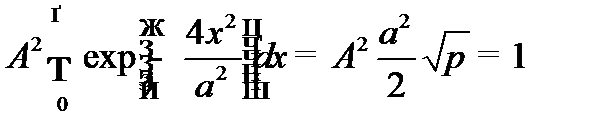
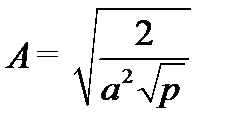
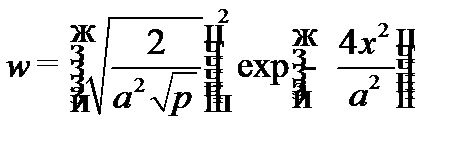
2. Эффективной областью локализации частицы называется пространство, в границах которого плотность вероятности нахождения частицы убывает в е раз.



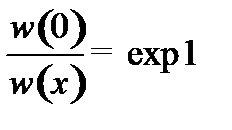 , где
, где 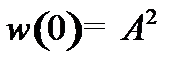
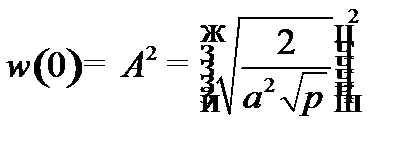
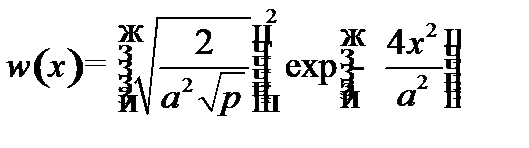
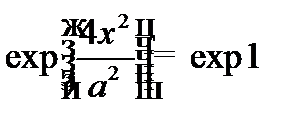 ;
; 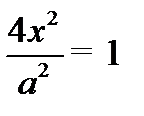
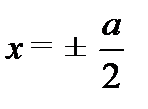 ;
; 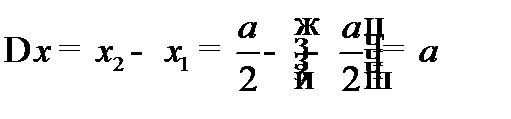
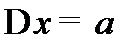
Задача 6
Частица массой m находится в бесконечно глубокой двумерной потенциальной яме с абсолютно непроницаемыми стенками. Найти возможные значения энергии, если стенки ямы равны 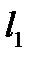 и
и 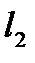 .
.
Решение:
Для двумерной ямы уравнение Шредингера имеет вид:
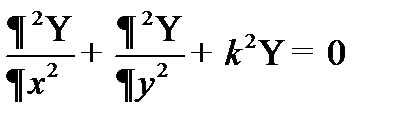 ; где
; где 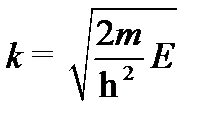
Решение ищем в виде: 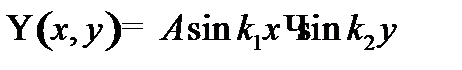 .
.
За точку отсчета примем один из углов ямы 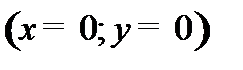 .
.
Из граничных условий:
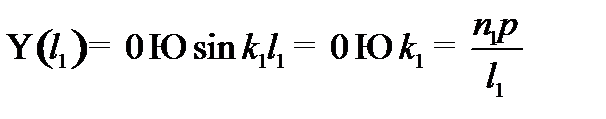 ;
;
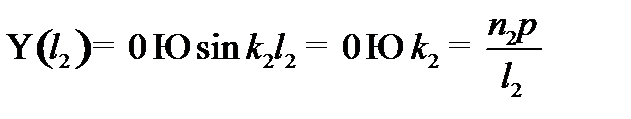


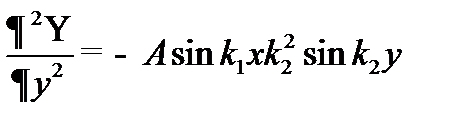
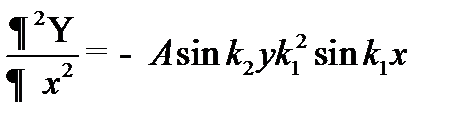
Подставив выражения для производных в уравнение Шредингера, получим:
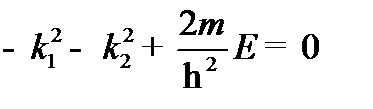
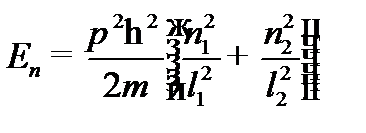 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|